FElupe documentation

FElupe is a Python 3.8+ 🐍 finite element analysis package 📦 focussing on the formulation and numerical solution of nonlinear problems in continuum mechanics 🔧 of solid bodies 🚂. Its name is a combination of FE (finite element) and the german word Lupe 🔍 (magnifying glass) as a synonym for getting an insight 📖 how a finite element analysis code 🧮 looks like under the hood 🕳️.

🏃 Beginner’s Guide

New to FElupe? The Beginner’s Guide contains an introduction to the concept of FElupe.

📖 API reference

The reference guide contains a detailed description of the FElupe API. It describes how the methods work and which parameters can be used. Requires an understanding of the key concepts.

☎ How-To

Step-by-step guides for specific tasks or problems with a focus on practical usability instead of completeness. Requires an understanding of the key concepts.

📚 Examples

A gallery of examples.

Highlights

• high-level finite-element-analysis API

• flexible building blocks for finite element assembly

• hyperelastic integral (weak) forms

• straight-forward definition of mixed-fields

• nearly-incompressible hyperelastic solid bodies

Installation

Install Python, fire up 🔥 a terminal and run 🏃

pip install felupe[all]

where [all] is a combination of [io,parallel,plot,progress,view] and installs all optional dependencies. FElupe has minimal requirements, all available at PyPI supporting all platforms.

• numpy for array operations

• scipy for sparse matrices

• tensortrax for automatic differentiation

In order to make use of all features of FElupe 💎💰💍👑💎, it is suggested to install all optional dependencies.

• einsumt for parallel (threaded) assembly

• h5py for writing XDMF result files

• matplotlib for plotting graphs

• meshio for mesh-related I/O

• pyvista for interactive visualizations

• tqdm for showing progress bars during job evaluations

Extension Packages

The capabilities of FElupe may be enhanced with extension packages created by the community.

Package	Description
hyperelastic	Constitutive hyperelastic material formulations
matadi	Material Definition with Automatic Differentiation (AD)
tensortrax	Math on Hyper-Dual Tensors with Trailing Axes (bundled with FElupe)
feplot	A visualization tool for FElupe

Performance

This is a simple benchmark to compare assembly times for linear elasticity and hyperelasticity on tetrahedrons.

Assembly Runtimes

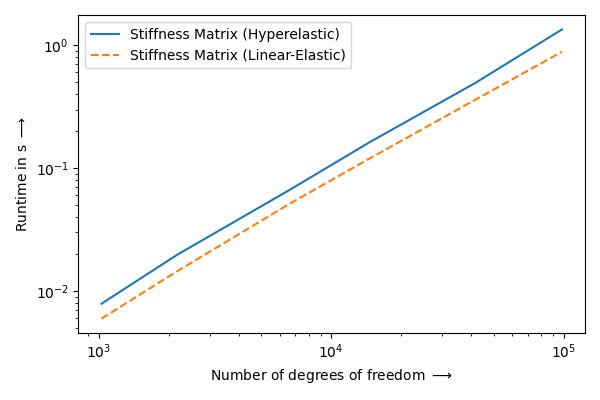
Analysis	DOF/s
Linear-Elastic	136193 +/-22916
Hyperelastic	100613 +/-18702

Tested on: Windows 10, Python 3.11, Intel® Core™ i7-11850H @ 2.50GHz, 32GB RAM.

Source Code

from timeit import timeit

import matplotlib.pyplot as plt
import numpy as np

import felupe as fem


def pre_linear_elastic(n, **kwargs):
   mesh = fem.Cube(n=n).triangulate()
   region = fem.RegionTetra(mesh)
   field = fem.FieldContainer([fem.Field(region, dim=3)])
   umat = fem.LinearElastic(E=1, nu=0.3)
   solid = fem.SolidBody(umat, field)
   return mesh, solid


def pre_hyperelastic(n, **kwargs):
   mesh = fem.Cube(n=n).triangulate()
   region = fem.RegionTetra(mesh)
   field = fem.FieldContainer([fem.Field(region, dim=3)])
   umat = fem.NeoHookeCompressible(mu=1.0, lmbda=2.0)
   solid = fem.SolidBody(umat, field)
   return mesh, solid


print("# Assembly Runtimes")
print("")
print("|   DOF   | Linear-Elastic in s | Hyperelastic in s |")
print("| ------- | ------------------- | ----------------- |")

points_per_axis = np.round((np.logspace(3, 5, 6) / 3)**(1 / 3)).astype(int)

number = 3
parallel = False

runtimes = np.zeros((len(points_per_axis), 2))

for i, n in enumerate(points_per_axis):
   mesh, solid = pre_linear_elastic(n)
   matrix = solid.assemble.matrix(parallel=parallel)
   time_linear_elastic = (
      timeit(lambda: solid.assemble.matrix(parallel=parallel), number=number) / number
   )

   mesh, solid = pre_hyperelastic(n)
   matrix = solid.assemble.matrix(parallel=parallel)
   time_hyperelastic = (
      timeit(lambda: solid.assemble.matrix(parallel=parallel), number=number) / number
   )

   runtimes[i] = time_linear_elastic, time_hyperelastic

   print(
      f"| {mesh.points.size:7d} | {runtimes[i][0]:19.2f} | {runtimes[i][1]:17.2f} |"
   )

dofs_le = points_per_axis ** 3 * 3 / runtimes[:, 0]
dofs_he = points_per_axis ** 3 * 3 / runtimes[:, 1]

print("")
print("| Analysis       |        DOF/s      |")
print("| -------------- | ----------------- |")
print(
   f"| Linear-Elastic |   {np.mean(dofs_le):5.0f} +/-{np.std(dofs_le):5.0f}  |"
)
print(f"| Hyperelastic   |   {np.mean(dofs_he):5.0f} +/-{np.std(dofs_he):5.0f}  |")

plt.figure()
plt.loglog(
   points_per_axis ** 3 * 3,
   runtimes[:, 1],
   "C0",
   label=r"Stiffness Matrix (Hyperelastic)",
)
plt.loglog(
   points_per_axis ** 3 * 3,
   runtimes[:, 0],
   "C1--",
   label=r"Stiffness Matrix (Linear-Elastic)",
)
plt.xlabel(r"Number of degrees of freedom $\longrightarrow$")
plt.ylabel(r"Runtime in s $\longrightarrow$")
plt.legend()
plt.tight_layout()
plt.savefig("benchmark.png")

Contents:

• Beginner’s Guide
• Examples
• How-To Guides
• API Reference

License

FElupe - Finite Element Analysis (C) 2021-2024 Andreas Dutzler, Graz (Austria).

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see https://www.gnu.org/licenses/.

Indices and tables

• Index

• Module Index

• Search Page