Ctrl+K

Mesh#

This module contains meshing-related classes and functions. Standalone mesh-tools (functions) are also available as mesh-methods.

Core

Mesh(points, cells[, cell_type])

A mesh with points, cells and optional a specified cell type.

MeshContainer(meshes[, merge, decimals])

A container which operates on a list of meshes with identical dimensions.

Geometries

Point([a])

A mesh with a single vertex point located at a.

mesh.Line([a, b, n])

A 1d-mesh with lines between a and b with n points.

Rectangle([a, b, n])

A rectangular 2d-mesh with quads between a and b with n points per axis.

Cube([a, b, n])

A cube shaped 3d-mesh with hexahedrons between a and b with n points per axis.

Grid(*xi[, indexing])

A grid shaped 3d-mesh with hexahedrons.

Circle([radius, centerpoint, n, sections, ...])

A circular shaped 2d-mesh with quads and n points on the circumferential edge of a 45-degree section.

mesh.Triangle([a, b, c, n, decimals])

A triangular shaped 2d-mesh with quads and n points at the edges of the three sub-quadrilaterals.

mesh.RectangleArbitraryOrderQuad([a, b, order])

A rectangular 2d-mesh with an arbitrarr-order Lagrange quad between a and b.

mesh.CubeArbitraryOrderHexahedron([a, b, order])

A rectangular 2d-mesh with an arbitrarr-order Lagrange hexahedron between a and b.

Tools

mesh.expand(points, cells, cell_type[, n, ...])

Expand a 0d-Point to a 1d-Line, a 1d-Line to a 2d-Quad or a 2d-Quad to a 3d-Hexahedron Mesh.

mesh.translate(points, cells, cell_type, ...)

Translate (move) a Mesh along a given axis.

mesh.rotate(points, cells, cell_type, ...[, ...])

Rotate a Mesh.

mesh.revolve(points, cells, cell_type[, n, ...])

Revolve a 0d-Point to a 1d-Line, a 1d-Line to 2d-Quad or a 2d-Quad to a 3d-Hexahedron Mesh.

mesh.sweep(points, cells, cell_type[, decimals])

Merge duplicate points and update cells of a Mesh.

mesh.mirror(points, cells, cell_type[, ...])

Mirror points by plane normal and ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

mesh.merge_duplicate_points(points, cells, ...)

Merge duplicate points and update cells of a Mesh.

mesh.merge_duplicate_cells(points, cells, ...)

Merge duplicate cells of a Mesh.

mesh.concatenate(meshes)

Join a sequence of meshes with identical cell types.

mesh.runouts(points, cells, cell_type[, ...])

Add simple rubber-runouts for realistic rubber-metal structures.

mesh.triangulate(points, cells, cell_type[, ...])

Triangulate a quad or a hex mesh.

mesh.convert(points, cells, cell_type[, ...])

Convert a mesh to a given order.

mesh.collect_edges(points, cells, cell_type)

Collect all unique edges, calculate and return midpoints on edges as well as the additional cells array.

mesh.collect_faces(points, cells, cell_type)

Collect all unique faces, calculate and return midpoints on faces as well as the additional cells array.

mesh.collect_volumes(points, cells, cell_type)

Collect all volumes, calculate and return midpoints on volumes as well as the additional cells array.

mesh.add_midpoints_edges(points, cells, ...)

Add midpoints on edges for given points and cells and update cell_type accordingly.

mesh.add_midpoints_faces(points, cells, ...)

Add midpoints on faces for given points and cells and update cell_type accordingly.

mesh.add_midpoints_volumes(points, cells, ...)

Add midpoints on volumes for given points and cells and update cell_type accordingly.

mesh.flip(points, cells, cell_type[, mask])

Ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

mesh.fill_between(mesh, other_mesh[, n])

Fill a 2d-Quad Mesh between two 1d-Line Meshes, embedded in 2d-space, or a 3d-Hexahedron Mesh between two 2d-Quad Meshes, embedded in 3d-space, by expansion.

mesh.dual(points, cells, cell_type[, ...])

Create a new dual mesh with given points per cell.

mesh.stack(meshes)

Stack cell-blocks from meshes with identical points-array and cell-types.

mesh.read(filename[, file_format, ...])

Read a mesh from a file using meshio.read() and create a MeshContainer.

Detailed API Reference

class felupe.Mesh(points, cells, cell_type=None)[source]#

A mesh with points, cells and optional a specified cell type.

Parameters:

  • points (ndarray) – Point coordinates.

  • cells (ndarray) – Point-connectivity of cells.

  • cell_type (str or None, optional) – An optional string in VTK-convention that specifies the cell type (default is None). Necessary when a mesh is saved to a file.

points#

Point coordinates.

Type:

ndarray

cells#

Point-connectivity of cells.

Type:

ndarray

cell_type#

A string in VTK-convention that specifies the cell type.

Type:

str or None

npoints#

Amount of points.

Type:

int

dim#

Dimension of mesh point coordinates.

Type:

int

ndof#

Amount of degrees of freedom.

Type:

int

ncells#

Amount of cells.

Type:

int

points_with_cells#

Array with points connected to cells.

Type:

ndarray

points_without_cells#

Array with points not connected to cells.

Type:

ndarray

cells_per_point#

Array which counts connected cells per point. Used for averaging results.

Type:

ndarray

Examples

>>> import numpy as np
>>> import felupe as fem
>>>
>>> points = np.array(
...     [[0.0, 0.0], [0.5, 0.1], [1.0, 0.2], [0.0, 1.0], [0.5, 0.9], [1.0, 0.8]]
... )
>>> cells = np.array([[0, 1, 4, 3], [1, 2, 5, 4]])
>>> mesh = fem.Mesh(points, cells, cell_type="quad")
>>>
>>> mesh.plot().show()
../_images/mesh-1_00_00.png

See also

felupe.MeshContainer

A container which operates on a list of meshes with identical dimensions.

felupe.Rectangle

A rectangular 2d-mesh with quads between a and b with n points per axis.

felupe.Cube

A cube shaped 3d-mesh with hexahedrons between a and b with n points per axis.

felupe.Grid

A grid shaped 3d-mesh with hexahedrons. Basically a wrapper for numpy.meshgrid() with default indexing="ij".

felupe.Circle

A circular shaped 2d-mesh with quads and n points on the circumferential edge of a 45-degree section. 90-degree sections are placed at given angles in degree.

felupe.mesh.Triangle

A triangular shaped 2d-mesh with quads and n points at the edges of the three sub-quadrilaterals.

add_midpoints_edges(cell_type=None)[source]#

Add midpoints on edges for given points and cells and update cell_type accordingly.

Parameters:

cell_type (str or None, optional) – A string in VTK-convention that specifies the new cell type (default is None). If None, the cell type is chosen automatically.

Returns:

A new mesh with inserted midpoints on cell edges.

Return type:

Mesh

Examples

Convert a mesh of hexahedrons to quadratic hexahedrons by inserting midpoints on the cell edges.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=6)
>>> mesh_with_midpoints_edges = mesh.add_midpoints_edges()
>>>
>>> mesh_with_midpoints_edges.plot(
...     plotter=mesh.plot(), style="points", color="black"
... ).show()
../_images/mesh-2_00_00.png 
>>> mesh_with_midpoints_edges
<felupe Mesh object>
  Number of points: 96
  Number of cells:
    quad8: 25

See also

felupe.mesh.add_midpoints_edges

Add midpoints on edges for given points and cells and update cell_type accordingly.

add_midpoints_faces(cell_type=None)[source]#

Add midpoints on faces for given points and cells and update cell_type accordingly.

Parameters:

cell_type (str or None, optional) – A string in VTK-convention that specifies the new cell type (default is None). If None, the cell type is chosen automatically.

Returns:

A new mesh with inserted midpoints on cell faces.

Return type:

Mesh

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=6)
>>> mesh_with_midpoints_faces = mesh.add_midpoints_faces(cell_type="quad")
>>>
>>> mesh_with_midpoints_faces.plot(
...     plotter=mesh.plot(), style="points", color="black"
... ).show()
../_images/mesh-3_00_00.png 
>>> mesh_with_midpoints_faces
<felupe Mesh object>
  Number of points: 61
  Number of cells:
    quad: 25

See also

felupe.mesh.add_midpoints_faces

Add midpoints on faces for given points and cells and update cell_type accordingly.

add_midpoints_volumes(cell_type=None)[source]#

Add midpoints on volumes for given points and cells and update cell_type accordingly.

Parameters:

cell_type (str or None, optional) – A string in VTK-convention that specifies the new cell type (default is None). If None, the cell type is chosen automatically.

Returns:

A new mesh with inserted midpoints on cell volumes.

Return type:

Mesh

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=6)
>>> mesh_with_midpoints_volumes = fem.mesh.add_midpoints_volumes(
...     mesh, cell_type_new="hexahedron9"
... )
>>>
>>> plotter = mesh.plot(opacity=0.5)
>>> actor = plotter.add_points(mesh_with_midpoints_volumes.points, color="black")
>>> plotter.show()

>>> mesh_with_midpoints_volumes
<felupe Mesh object>
  Number of points: 341
  Number of cells:
    hexahedron9: 125

See also

felupe.mesh.add_midpoints_volumes

Add midpoints on volumes for given points and cells and update cell_type accordingly.

add_runouts(values=[0.1, 0.1], centerpoint=[0, 0, 0], axis=0, exponent=5, mask=slice(None, None, None), normalize=False)[source]#

Add simple rubber-runouts for realistic rubber-metal structures.

Parameters:

  • values (list or ndarray, optional) – Relative amount of runouts (per coordinate) perpendicular to the axis (default is 10% per coordinate, i.e. [0.1, 0.1]).

  • centerpoint (list or ndarray, optional) – Center-point coordinates (default is [0, 0, 0]).

  • axis (int or None, optional) – Axis (default is 0).

  • exponent (int, optional) – Positive exponent to control the shape of the runout. The higher the exponent, the steeper the transition (default is 5).

  • mask (list or None, optional) – List of points to be considered (default is None).

  • normalize (bool, optional) – Normalize the runouts to create indents, i.e. maintain the original shape at the ends (default is False).

Returns:

The mesh with the modified point coordinates.

Return type:

Mesh

Examples

>>> import felupe as fem
>>>
>>> rect = fem.Rectangle(a=(-3, -1), b=(3, 1), n=(31, 11))
>>> mesh = rect.add_runouts(axis=1, values=[0.2], normalize=True)
>>>
>>> mesh.plot().show()
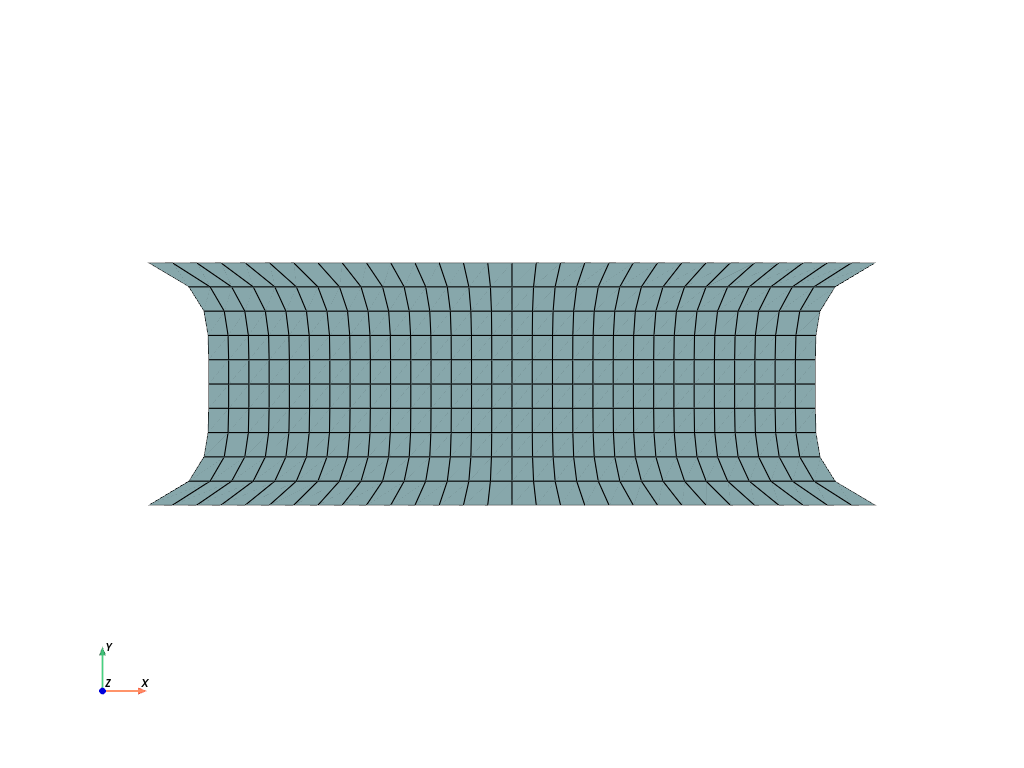
../_images/mesh-5_00_00.png 
>>> import felupe as fem
>>>
>>> cube = fem.Cube(a=(-3, -2, -1), b=(3, 2, 1), n=(31, 21, 11))
>>> mesh = cube.add_runouts(axis=2, values=[0.1, 0.3], normalize=True)
>>>
>>> mesh.plot().show()
../_images/mesh-6_00_00.png

See also

felupe.mesh.runouts

Add simple rubber-runouts for realistic rubber-metal structures.

as_meshio(**kwargs)[source]#

Export the mesh as meshio.Mesh.

Parameters:

**kwargs (dict, optional) – Additional keyword-arguments for meshio.Mesh(points, cells, **kwargs).

Returns:

The mesh as meshio.Mesh.

Return type:

meshio.Mesh

as_pyvista(cell_type=None, **kwargs)[source]#

Export the mesh as pyvista.UnstructuredGrid.

Parameters:

  • cell_type (pyvista.CellType or None, optional) – Cell-type of PyVista (default is None).

  • **kwargs (dict, optional) – Additional keyword-arguments for pyvista.UnstructuredGrid.

Returns:

The mesh as pyvista.UnstructuredGrid.

Return type:

pyvista.UnstructuredGrid

collect_edges(cells, cell_type)#

Collect all unique edges, calculate and return midpoints on edges as well as the additional cells array.

See also

felupe.mesh.add_midpoints_edges

Add midpoints on cell edges for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_edges

Add midpoints on cell edges for given points and cells and update cell_type accordingly.

collect_faces(cells, cell_type)#

Collect all unique faces, calculate and return midpoints on faces as well as the additional cells array.

See also

felupe.mesh.add_midpoints_faces

Add midpoints on cell faces for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_faces

Add midpoints on cell faces for given points and cells and update cell_type accordingly.

collect_volumes(cells, cell_type)#

Collect all volumes, calculate and return midpoints on volumes as well as the additional cells array.

See also

felupe.mesh.add_midpoints_volumes

Add midpoints on cell volumes for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_volumes

Add midpoints on cell volumes for given points and cells and update cell_type accordingly.

convert(order=0, calc_points=False, calc_midfaces=False, calc_midvolumes=False)[source]#

Convert a mesh to a given order. Only conversions to order=0 and order=2 are supported. This function supports meshes with cell types "triangle", "tetra", "quad" and "hexahedron".

Parameters:

  • order (int, optional) – The order of the converted mesh (default is 0). If 0, the points-array will be of shape (ncells, dim). If 0 and calc_points is True, the mean of all points per cell is evaluated. If 0 and calc_points is False, the points array is filled with zeros. If 2, at least midpoints on cell edges are added to the mesh. If 2 and calc_midfaces is True, midpoints on cell faces are also added. If 2 and calc_midvolumes is True, midpoints on cell volumes are also added. Raises an error if not 0 or 2.

  • calc_points (bool, optional) – Flag to return the mean of all points per cell if order=0 (default is False). If False, the points-array is filled with zeros.

  • calc_midfaces (bool, optional) – Flag to add midpoints on cell faces if order=2 (default is False).

  • calc_midvolumes (bool, optional) – Flag to add midpoints on cell volumes if order=2 (default is False).

Returns:

The converted mesh.

Return type:

Mesh

Examples

Convert a mesh of hexahedrons to quadratic hexahedrons by inserting midpoints on the cell edges.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=6)
>>> mesh2 = mesh.convert(order=2)
>>>
>>> plotter = mesh2.plot(plotter=mesh.plot(), style="points", color="black")
>>> plotter.show()

>>> mesh2
<felupe Mesh object>
  Number of points: 96
  Number of cells:
    quad8: 25

See also

felupe.mesh.add_midpoints_edges

Add midpoints on edges for given points and cells and update cell_type accordingly.

felupe.mesh.add_midpoints_faces

Add midpoints on faces for given points and cells and update cell_type accordingly.

felupe.mesh.add_midpoints_volumes

Add midpoints on volumes for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_edges

Add midpoints on edges for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_faces

Add midpoints on faces for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_volumes

Add midpoints on volumes for given points and cells and update cell_type accordingly.

copy(points=None, cells=None, cell_type=None)#

Return a deepcopy.

disconnect(points_per_cell=None, calc_points=True)[source]#

Return a new instance of a Mesh with disconnected cells. Optionally, the points-per-cell may be specified (must be lower or equal the number of points- per-cell of the original Mesh). If the Mesh is to be used as a dual Mesh, then the point-coordinates do not have to be re-created because they are not used.

See also

felupe.Mesh.dual

Create a new dual mesh with given points per cell.

dual(points_per_cell=None, disconnect=True, calc_points=False, offset=0, npoints=None)[source]#

Create a new dual mesh with given points per cell.

Parameters:

  • points_per_cell (int or None, optional) – Number of points per cell, must be equal or lower than cells.shape[1] ( default is None). If None, all points per cell are considered for the dual mesh.

  • disconnect (bool, optional) – A flag to disconnect the mesh (each cell has its own points). Default is True.

  • calc_points (bool, optional) – A flag to calculate the point coordinates for the dual mesh (default is False). If False, the points array is filled with zeros.

  • offset (int, optional) – An offset to be added to the cells array (default is 0).

  • npoints (int or None, optional) – Number of points for the dual mesh. If the given number of points is greater than npoints * points_per_cell, then the missing points are added to the points array (filled with zeros). Default is None.

Returns:

The dual mesh.

Return type:

Mesh

Notes

Note

The points array of the dual mesh always has a shape of (npoints * points_per_cell, dim).

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=5).add_midpoints_edges()
>>> region = fem.RegionQuadraticQuad(mesh=mesh)
>>>
>>> mesh_dual = mesh.dual(points_per_cell=1, disconnect=False)
>>> region_dual = fem.RegionConstantQuad(
...     mesh_dual, quadrature=region.quadrature, grad=False
... )
>>>
>>> displacement = fem.FieldPlaneStrain(region, dim=2)
>>> pressure = fem.Field(region_dual)
>>> field = fem.FieldContainer([displacement, pressure])

See also

felupe.mesh.dual

Create a new dual mesh with given points per cell.

expand(n=11, z=1, axis=-1, expand_dim=True)[source]#

Expand a 0d-Point to a 1d-Line, a 1d-Line to a 2d-Quad or a 2d-Quad to a 3d-Hexahedron Mesh.

Parameters:

  • n (int, optional) – Number of n-point repetitions or (n-1)-cell repetitions, default is 11. Must be greater than 0.

  • z (float or ndarray, optional) – Total expand dimension as float (edge length in expand direction is z / n), default is 1. Optionally, if an array is passed these entries are taken as expansion and n is ignored.

  • axis (int, optional) – Axis of expansion (default is -1).

  • mask (ndarray or None, optional) – A boolean mask to select points which are rotated (default is None).

  • expand_dim (bool, optional) – Expand the dimension of the point coordinates (default is True).

Returns:

The expanded mesh.

Return type:

Mesh

Examples

Expand a rectangle to a cube.

>>> import felupe as fem
>>>
>>> rect = fem.Rectangle(n=4)
>>> cube = rect.expand(n=7, z=2)
>>>
>>> cube.plot().show()
../_images/mesh-8_00_00.png 
>>> cube
<felupe Mesh object>
  Number of points: 112
  Number of cells:
    hexahedron: 54

See also

felupe.mesh.expand

Expand a 0d-Point to a 1d-Line, a 1d-Line to a 2d-Quad or a 2d-Quad to a 3d-Hexahedron Mesh.

fill_between(other_mesh, n=11)[source]#

Fill a 2d-Quad Mesh between two 1d-Line Meshes, embedded in 2d-space, or a 3d-Hexahedron Mesh between two 2d-Quad Meshes, embedded in 3d-space, by expansion. Both meshes must have equal number of points and cells. The cells-array is taken from the first mesh.

Parameters:

  • other_mesh (felupe.Mesh) – The other line- or quad-mesh.

  • n (int or ndarray) – Number of n-point repetitions or (n-1)-cell repetitions, (default is 11). If an array is given, then its values are used for the relative positions in a reference configuration (-1, 1) between the two meshes.

Returns:

The expanded mesh.

Return type:

felupe.Mesh

Examples

>>> import felupe as fem
>>>
>>> inner = fem.mesh.revolve(fem.Point(1)).expand(z=0.4).translate(0.2, axis=2)
>>> outer = fem.mesh.revolve(fem.Point(2), phi=160).rotate(
...     axis=2, angle_deg=20
... ).expand(z=1.2)
>>> mesh = inner.fill_between(outer, n=6)
>>>
>>> mesh.plot().show()
../_images/mesh-9_00_00.png

See also

felupe.mesh.fill_between

Fill a 2d-Quad Mesh between two 1d-Line Meshes, embedded in 2d-space, or a 3d-Hexahedron Mesh between two 2d-Quad Meshes, embedded in 3d-space, by expansion.

flip(mask=None)[source]#

Ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

Parameters:

mask (list, ndarray or None, optional) – Boolean mask for selected cells to flip (default is None). If None, all cells are selected to be flipped.

Returns:

The mesh with a rearranged cells array to ensure positive cell volumes.

Return type:

Mesh

Examples

A quad mesh with negative cell volumes occurs if one coordinate axis is multiplied by -1. The error pops up if a region is created with this mesh.

>>> import numpy as np
>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=3)
>>> mesh.update(points=mesh.points * np.array([[-1, 1]]))
>>> region = fem.RegionQuad(mesh)

The sum of the differential volumes \(V = \sum_c \sum_q dV_{qc}\) is evaluated to -1.0.

>>> region.dV.sum()
-1.0

Let’s try to fix the mesh.

>>> mesh.cells
array([[0, 1, 4, 3],
       [1, 2, 5, 4],
       [3, 4, 7, 6],
       [4, 5, 8, 7]])

The cells array is rearranged to ensure positive cell volumes.

>>> mesh_fixed = mesh.flip()
>>> mesh_fixed.cells
array([[3, 4, 1, 0],
       [4, 5, 2, 1],
       [6, 7, 4, 3],
       [7, 8, 5, 4]])

A region now correctly evaluates the total volume of the mesh to 1.0.

>>> region_fixed = fem.RegionQuad(mesh_fixed)
>>> region_fixed.dV.sum()
1.0

See also

felupe.mesh.flip

Ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

get_cell_ids(point_ids)[source]#

Return cell ids which have the given point ids in their connectivity.

Parameters:

point_ids (list or ndarray) – Array with point ids which are used to search for cells.

Returns:

Array with cell ids which have the given point ids in their connectivity.

Return type:

ndarray

Examples

>>> import numpy as np
>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=11)
>>> point_ids = mesh.get_point_ids([0, 1, 1])
>>> point_ids
array([1320])

>>> cell_ids = mesh.get_cell_ids(point_ids)
>>> cell_ids
array([990])
get_cell_ids_neighbours(cell_ids)[source]#

Return cell ids which share points with given cell ids.

Parameters:

cell_ids (list or ndarray) – Array with cell ids which are used to search for neighbour cells.

Returns:

Array with cell ids which are next to the given cells.

Return type:

ndarray

Examples

>>> import numpy as np
>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=11)
>>> point_ids = mesh.get_point_ids([0, 1, 1])
>>> point_ids
array([1320])

>>> cell_ids = mesh.get_cell_ids(point_ids)
>>> cell_ids
array([990])

Find the cell ids which share at least one point with the given cell id(s).

>>> cell_ids_neighbours = mesh.get_cell_ids_neighbours(cell_ids)
>>> cell_ids_neighbours
array([880, 881, 890, 891, 980, 981, 990, 991])
get_point_ids(value, fun=<function isclose>, mode=<function all>, **kwargs)[source]#

Return point ids for points which are close to a given value.

Parameters:

  • value (float, list or ndarray) – Scalar value or point coordinates.

  • fun (callable, optional) – The function used to compare the points to the given value, i.e. with a function signature fun(mesh.points, value, **kwargs). Default is numpy.isclose().

  • mode (callable, optional) – A callable used to combine the search results, either numpy.any() or numpy.all().

  • **kwargs (dict, optional) – Additional keyword arguments for fun(mesh.points, value, **kwargs).

Returns:

Array with point ids.

Return type:

ndarray

Examples

Get point ids at given coordinates for a mesh with duplicate points.

>>> import numpy as np
>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=11)
>>> mesh.update(points=np.vstack([mesh.points, mesh.points]))
>>> point_ids = mesh.get_point_ids([0, 1, 1])
>>> point_ids
array([1320, 2651])

>>> mesh.points[point_ids]
array([[0., 1., 1.],
       [0., 1., 1.]])
get_point_ids_corners()[source]#

Return point ids which are located at (xmin, ymin), (xmax, ymin), etc.

Returns:

Array with point ids which are located at the corners.

Return type:

ndarray

Examples

>>> import numpy as np
>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=11)
>>> point_ids_corners = mesh.get_point_ids_corners()
>>> point_ids_corners
array([   0, 1210,   10, 1220,  110, 1320,  120, 1330])
get_point_ids_shared(cell_ids_neighbours)[source]#

Return shared point ids for given cell ids.

Parameters:

cells_neighbours (list or ndarray) – Array with cell ids.

Returns:

Array with point ids which are connected to all given cell neighbours.

Return type:

ndarray

Examples

>>> import numpy as np
>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=11)
>>> point_ids = mesh.get_point_ids([0, 1, 1])
>>> point_ids
array([1320])

>>> cell_ids = mesh.get_cell_ids(point_ids)
>>> cell_ids
array([990])

Find the cell ids which share at least one point with the given cell id(s).

>>> cell_ids_neighbours = mesh.get_cell_ids_neighbours(cell_ids)
>>> cell_ids_neighbours
array([880, 881, 890, 891, 980, 981, 990, 991])

Find the shared point ids for the list of cell ids.

>>> point_ids_shared = mesh.get_point_ids_shared(cell_ids_neighbours)
>>> point_ids_shared
array([1189])
imshow(*args, ax=None, **kwargs)[source]#

Take a screenshot of the mesh, show the image data in a figure and return the ax.

merge_duplicate_cells(cells, cell_type)#

Merge duplicate cells of a Mesh.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

Returns:

  • points (ndarray) – Point coordinates.

  • cells (list or ndarray) – Cells with merged duplicate cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Notes

Warning

This function re-sorts cells.

Note

This function does not merge duplicate points.

Examples

Two quad meshes to be merged overlap some cells. Merge these duplicated points and update the cells.

>>> import felupe as fem
>>>
>>> rect1 = fem.Rectangle(n=11)
>>> rect2 = fem.Rectangle(a=(0.9, 0), b=(1.9, 1), n=11)
>>>
>>> container = fem.MeshContainer([rect1, rect2])
>>> stack = fem.mesh.stack(container.meshes)
>>> mesh = fem.mesh.merge_duplicate_points(stack)
>>>
>>> mesh.plot(opacity=0.6).show()
../_images/mesh-10_00_00.png

Each mesh contains 121 points and 100 cells.

>>> rect1
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

>>> rect2
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

These two meshes are now stored in a MeshContainer.

>>> container
<felupe mesh container object>
  Number of points: 242
  Number of cells:
    quad: 100
    quad: 100

The meshes of the mesh container are stacked.

>>> stack
<felupe Mesh object>
  Number of points: 242
  Number of cells:
    quad: 200

After merging the duplicated points and cells, the number of points is reduced but the number of cells is unchanged.

>>> mesh
<felupe Mesh object>
  Number of points: 220
  Number of cells:
    quad: 200

Note

The MeshContainer may be directly created with merge=True. This enforces merge_duplicate_points() for the shared points array of the container.

The duplicate cells are merged in a second step.

>>> merged = fem.mesh.merge_duplicate_cells(mesh)
>>> merged
<felupe Mesh object>
  Number of points: 220
  Number of cells:
    quad: 190
felupe/images/mesh_merged.png

See also

felupe.Mesh.merge_duplicate_points

Merge duplicate points of a Mesh.

felupe.Mesh.merge_duplicate_cells

Merge duplicate cells of a Mesh.

felupe.MeshContainer

A container which operates on a list of meshes with identical dimensions.

merge_duplicate_points(decimals=None)[source]#

Merge duplicate points and update cells of a Mesh.

Parameters:

decimals (int or None, optional) – Number of decimals for point coordinate comparison (default is None).

Returns:

The mesh with merged duplicate points and updated cells.

Return type:

Mesh

Notes

Warning

This function re-sorts points.

Note

This function does not merge duplicate cells.

Examples

Two quad meshes to be merged overlap some points. Merge these duplicated points and update the cells.

>>> import felupe as fem

>>> rect1 = fem.Rectangle(n=11)
>>> rect2 = fem.Rectangle(a=(0.9, 0), b=(1.9, 1), n=11)
>>> rect2
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

Each mesh contains 121 points and 100 cells. These two meshes are now stored in a MeshContainer.

>>> container = fem.MeshContainer([rect1, rect2])
>>> container
<felupe mesh container object>
  Number of points: 242
  Number of cells:
    quad: 100
    quad: 100
felupe/images/mesh_container.png

The meshes of the mesh container are stacked.

>>> stack = fem.mesh.stack(container.meshes)
>>> stack
<felupe Mesh object>
  Number of points: 242
  Number of cells:
    quad: 200

After merging the duplicated points and cells, the number of points is reduced but the number of cells is unchanged.

>>> mesh = stack.merge_duplicate_points()
>>> mesh
<felupe Mesh object>
  Number of points: 220
  Number of cells:
    quad: 200

>>> ax = mesh.imshow(opacity=0.6)
felupe/images/mesh_sweep.png

Note

The MeshContainer may be directly created with merge=True. This enforces merge_duplicate_points() for the shared points array of the container.

See also

felupe.mesh.merge_duplicate_points

Merge duplicated points and update cells of a Mesh.

felupe.MeshContainer

A container which operates on a list of meshes with identical dimensions.

mirror(normal=[1, 0, 0], centerpoint=[0, 0, 0], axis=None)[source]#

Mirror points by plane normal and ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

Parameters:

  • normal (list or ndarray, optional) – Mirror-plane normal vector (default is [1, 0, 0]).

  • centerpoint (list or ndarray, optional) – Center-point coordinates on the mirror plane (default is [0, 0, 0]).

  • axis (int or None, optional) – Mirror axis (default is None).

Returns:

The mirrored mesh.

Return type:

Mesh

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Circle(sections=[0, 90, 180], n=5)
>>> mesh.plot().show()
../_images/mesh-11_00_00.png 
>>> import felupe as fem
>>>
>>> mesh = fem.Circle(sections=[0, 90, 180], n=5)
>>> mesh.mirror(normal=[0, 1, 0]).plot().show()
../_images/mesh-12_00_00.png

See also

felupe.Mesh.mirror

Mirror points by plane normal and ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

modify_corners(point_ids=None)[source]#

Modify the corners of a regular rectangle (quad) or cube (hexahedron) inplace. Only the cells array is modified, the points array remains unchanged.

Parameters:

point_ids (ndarray or None, optional) – Array with point ids located at the corners which are modified (default is None). If None, all corners are modified.

Notes

Description of the algorithm:

  1. Get corner point ids.

For each corner point:

  1. Get attached cell and find cell neighours.

  2. Get the shared point of the cell and its neighbours.

  3. Get pair-wise shared points which are located on an edge.

  4. Replace the shared points with the corner point.

  5. Delete the cell attached to the corner point.

Examples

>>> import numpy as np
>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(b=(3, 1), n=(16, 6))
>>> mesh.plot().show()
../_images/mesh-13_00_00.png 
>>> mesh = mesh.modify_corners()  # inplace
>>> mesh.plot().show()
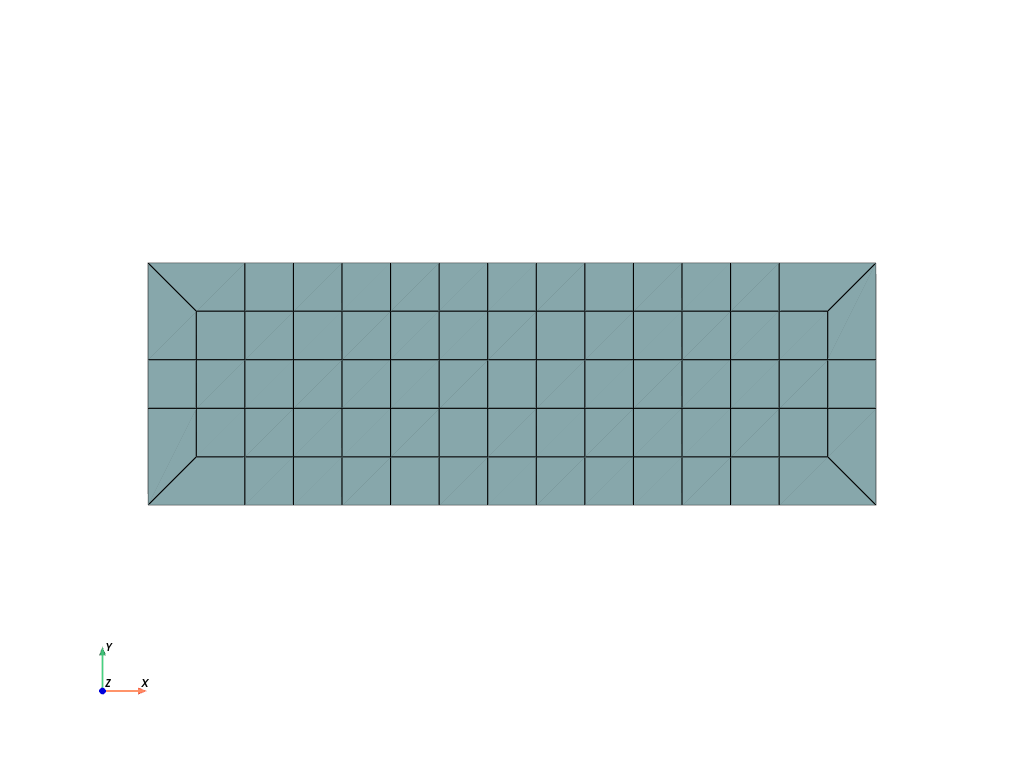
../_images/mesh-14_00_00.png
plot(*args, **kwargs)[source]#

Plot the mesh.

See also

felupe.Scene.plot

Plot method of a scene.

revolve(n=11, phi=180, axis=0, expand_dim=True)[source]#

Revolve a 2d-Quad to a 3d-Hexahedron Mesh.

Parameters:

  • n (int, optional) – Number of n-point revolutions (or (n-1) cell revolutions), default is 11.

  • phi (float or ndarray, optional) – Revolution angle in degree (default is 180).

  • axis (int, optional) – Revolution axis (default is 0).

  • expand_dim (bool, optional) – Expand the dimension of the point coordinates (default is True).

Returns:

The revolved mesh.

Return type:

Mesh

Examples

Revolve a cylinder from a rectangle.

>>> import felupe as fem
>>>
>>> rect = fem.Rectangle(a=(0, 4), b=(3, 5), n=(10, 4))
>>> mesh = rect.revolve(n=11, phi=180, axis=0)
>>> mesh.plot().show()
../_images/mesh-15_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 440
  Number of cells:
    hexahedron: 270

See also

felupe.mesh.revolve

Revolve a 2d-Quad to a 3d-Hexahedron Mesh.

rotate(angle_deg, axis, center=None, mask=None)[source]#

Rotate a Mesh.

Parameters:

  • angle_deg (int) – Rotation angle in degree.

  • axis (int) – Rotation axis.

  • center (list or ndarray or None, optional) – Center point coordinates (default is None).

  • mask (ndarray or None, optional) – A boolean mask to select points which are rotated (default is None).

Returns:

The rotated mesh.

Return type:

Mesh

Examples

Rotate a rectangle in the xy-plane by 35 degree.

>>> import felupe as fem
>>>
>>> rect = fem.Rectangle(b=(3, 1), n=(10, 4))
>>> mesh = rect.rotate(angle_deg=35, axis=2, center=[1.5, 0.5])
>>> mesh.plot().show()
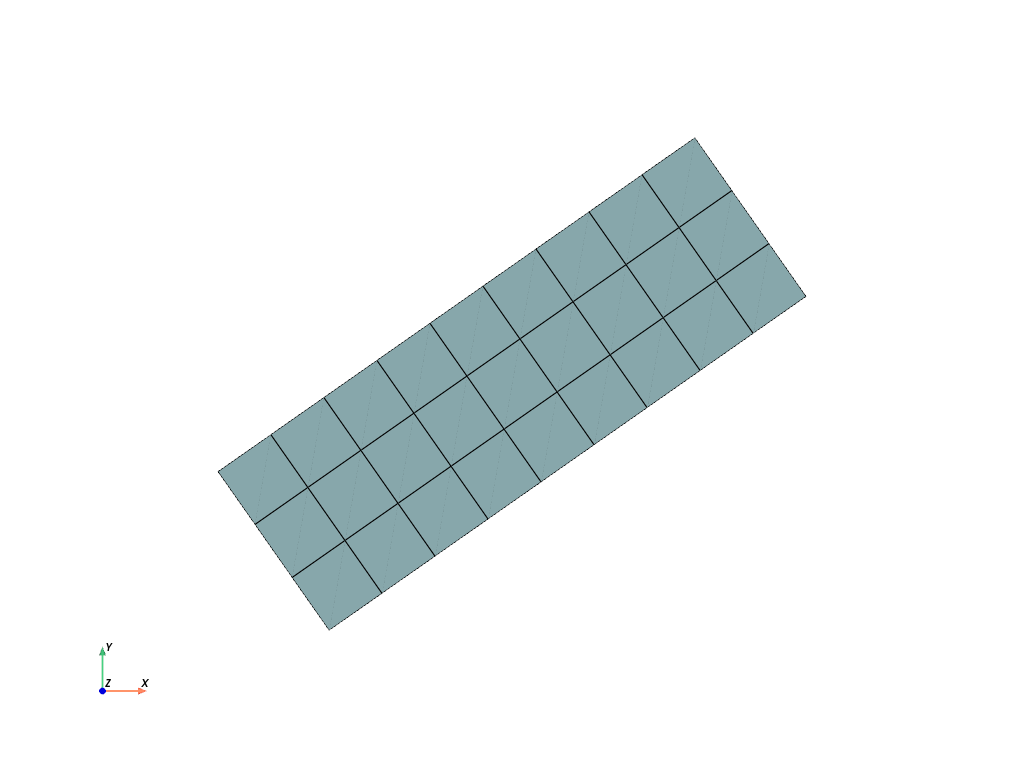
../_images/mesh-16_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 40
  Number of cells:
    quad: 27

See also

felupe.mesh.rotate

Rotate a Mesh.

screenshot(*args, filename='mesh.png', transparent_background=None, scale=None, **kwargs)[source]#

Take a screenshot of the mesh.

See also

pyvista.Plotter.screenshot

Take a screenshot of a PyVista plotter.

translate(move, axis)[source]#

Translate (move) a Mesh along a given axis.

Parameters:

  • move (float) – Translation along given axis.

  • axis (int) – Translation axis.

Returns:

The translated mesh.

Return type:

Mesh

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Circle(n=6)
>>> mesh.points.min(axis=0), mesh.points.max(axis=0)
(array([-1., -1.]), array([1., 1.]))

>>> translated = mesh.translate(0.3, axis=1)
>>> translated.points.min(axis=0), translated.points.max(axis=0)
(array([-1. , -0.7]), array([1. , 1.3]))

See also

felupe.mesh.translate

Translate (move) a Mesh along a given axis.

triangulate(mode=3)[source]#

Triangulate a quad or a hex mesh.

Parameters:

mode (int, optional) – Choose a mode how to convert hexahedrons to tets [1]_ (default is 3).

Returns:

The triangulated mesh.

Return type:

Mesh

Examples

Use mode=0 to convert a mesh of hexahedrons into tetrahedrons [1]_.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=6)
>>> mesh.triangulate(mode=0).plot().show()
../_images/mesh-17_00_00.png

Use mode=3 to convert a mesh of hexahedrons into tetrahedrons [1]_.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=6)
>>> mesh.triangulate(mode=3).plot().show()
../_images/mesh-18_00_00.png

References

See also

felupe.mesh.triangulate

Triangulate a quad or a hex mesh.

update(points=None, cells=None, cell_type=None, callback=None)#

Update the mesh with given points and cells arrays inplace. Optionally, a callback is evaluated.

Parameters:

  • points (ndarray or None) – New point coordinates (default is None). If None, it is unchanged.

  • cells (ndarray) – New point-connectivity of cells (default is None). If None, it is unchanged.

  • cell_type (str or None, optional) – New string in VTK-convention that specifies the cell type (default is None). If None, it is unchanged.

  • callback (callable or None, optional) – A callable which is called after the mesh is updated (default is None).

Examples

Warning

If the points of a mesh are modified and a region was already created with the mesh, it is important to re-evaluate (reload) the Region.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=6)
>>> region = fem.RegionHexahedron(mesh)
>>> field = fem.FieldContainer([fem.Field(region, dim=3)])
>>>
>>> new_points = mesh.rotate(angle_deg=-90, axis=2).points
>>> mesh.update(points=new_points, callback=region.reload)

See also

felupe.Region.reload

Reload the numeric region.

view(point_data=None, cell_data=None, cell_type=None)[source]#

View the mesh with optional given dicts of point- and cell-data items.

Parameters:

  • point_data (dict or None, optional) – Additional point-data dict (default is None).

  • cell_data (dict or None, optional) – Additional cell-data dict (default is None).

  • cell_type (pyvista.CellType or None, optional) – Cell-type of PyVista (default is None).

Returns:

A object which provides visualization methods for felupe.Mesh.

Return type:

felupe.ViewMesh

See also

felupe.ViewMesh

Visualization methods for Mesh.

write(filename='mesh.vtk', **kwargs)[source]#

Write the mesh to a file.

Parameters:

  • filename (str, optional) – The filename of the mesh (default is mesh.vtk).

  • **kwargs (dict, optional) – Additional keyword arguments for meshio.Mesh.write().

Notes

Note

For XDMF-export please ensure to have h5py (as an optional dependency of meshio) installed.

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=3)
>>> mesh.write(filename="mesh.vtk")

See also

felupe.mesh.read

Read a mesh from a file using meshio.read().

felupe.Mesh.write

Write the mesh to a file.

property x#

Return the first column (x-component) of the points array.

property y#

Return the second column (y-component) of the points array.

property z#

Return the third column (z-component) of the points array.

class felupe.MeshContainer(meshes, merge=False, decimals=None)[source]#

A container which operates on a list of meshes with identical dimensions.

Parameters:

  • meshes (list of Mesh) – A list of meshes which are organized by the mesh container.

  • merge (bool, optional) – Flag to merge duplicate mesh points. This changes the cells arrays of the meshes. Default is False.

  • decimals (float or None, optional) – Precision decimals for merging duplicated mesh points. Only relevant if merge=True. Default is None.

Notes

All meshes are modified to refer to the same points array. By default, the points arrays from the given list of meshes is concatenated and the cells arrays are modified accordingly. Optionally, the points array may be merged on duplicated points.

Examples

>>> import felupe as fem
>>>
>>> cube = fem.Cube(n=3)
>>> cylinder = fem.Circle().expand(n=2)
>>> mesh = fem.MeshContainer([cube, cylinder])
>>>
>>> mesh.plot().show()
../_images/mesh-19_00_00.png 
>>> mesh
<felupe mesh container object>
  Number of points: 61
  Number of cells:
    hexahedron: 8
    hexahedron: 12

The cells array of the second mesh starts with an offset

>>> mesh.meshes[1].cells.min()
27

identical to the number of points from the first mesh.

>>> cube.npoints
27

If the container is created with merge=True, then the number of points is lower than before.

>>> import felupe as fem
>>>
>>> cube = fem.Cube(n=3)
>>> cylinder = fem.Circle().expand(n=2)
>>> mesh = fem.MeshContainer([cube, cylinder], merge=True)
>>>
>>> mesh.plot().show()
../_images/mesh-20_00_00.png 
>>> mesh
<felupe mesh container object>
  Number of points: 51
  Number of cells:
    hexahedron: 8
    hexahedron: 12
append(mesh)[source]#

Append a Mesh to the list of meshes.

as_meshio(combined=True, **kwargs)[source]#

Export a (combined) mesh object as meshio.Mesh.

cells()[source]#

Return a list of tuples with cell-types and cell-connectivities.

copy()[source]#

Return a deepcopy of the mesh container.

imshow(*args, ax=None, dpi=None, **kwargs)[source]#

Take a screenshot of the meshes of the mesh container, show the image data in a figure and return the ax.

merge_duplicate_points(decimals=None)[source]#

Merge duplicate points and update the meshes.

plot(*args, colors=None, opacity=0.99, **kwargs)[source]#

Plot the meshes of the mesh container.

See also

felupe.Scene.plot

Plot method of a scene.

pop(index)[source]#

Pop an item of the list of meshes.

screenshot(*args, filename='mesh.png', transparent_background=None, scale=None, colors=None, opacity=0.99, **kwargs)[source]#

Take a screenshot of the meshes of the mesh container.

See also

pyvista.Plotter.screenshot

Take a screenshot of a PyVista plotter.

stack(idx=None)[source]#

Stack cell-blocks with same cell-types into a single mesh.

Parameters:

idx (list of int or None, optional) – List of mesh-indices to be stacked (default is None).

Returns:

The stacked mesh.

Return type:

Mesh

Notes

The points-array is taken from the first mesh. The cells-array of the stacked mesh is created by a vertical stack of the cells-arrays.

Examples

Two quad meshes with identical point arrays should be stacked into a single mesh.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=11)
>>> rect1, rect2 = mesh.copy(), mesh.copy()
>>> rect1.update(cells=mesh.cells[: 40])
>>> rect2.update(cells=mesh.cells[-50:])
>>> container = fem.MeshContainer([rect1, rect2])
>>> mesh = container.stack()
>>>
>>> mesh.plot().show()
../_images/mesh-21_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 242
  Number of cells:
    quad: 90

See also

felupe.mesh.stack

Stack cell-blocks from meshes with identical points-array and cell-types.

class felupe.Point(a=0.0)[source]#

Bases: Mesh

A mesh with a single vertex point located at a.

Parameters:

a (float, optional) – Vertex point coordinate of the mesh (default is 0.0).

Examples

>>> import felupe as fem

>>> mesh = fem.Point(a=-2.1)
>>> mesh
<felupe Mesh object>
  Number of points: 1
  Number of cells:
    vertex: 1

>>> mesh.points
array([[-2.1]])

>>> mesh.cells
array([[0]])
class felupe.mesh.Line(a=0.0, b=1.0, n=2)[source]#

Bases: Mesh

A 1d-mesh with lines between a and b with n points.

Parameters:

  • a (float, optional) – Left end point of the mesh (default is 0.0).

  • b (float, optional) – Right end point of the mesh (default is 1.0).

  • n (int, optional) – Number of points (default is 2).

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.mesh.Line(a=-2.1, b=3.5, n=3)
>>> mesh.plot().show()
../_images/mesh-22_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 3
  Number of cells:
    line: 2

>>> mesh.points
array([[-2.1],
       [ 0.7],
       [ 3.5]])

>>> mesh.cells
array([[0, 1],
       [1, 2]])
class felupe.Rectangle(a=(0.0, 0.0), b=(1.0, 1.0), n=(2, 2))[source]#

Bases: Mesh

A rectangular 2d-mesh with quads between a and b with n points per axis.

Parameters:

  • a (2-tuple of float, optional) – Lower-left end point of the mesh (default is (0.0, 0.0)).

  • b (2-tuple of float, optional) – Upper-right end point of the mesh (default is (1.0, 1.0)).

  • n (int or 2-tuple of int, optional) – Number of points per axis (default is (2, 2)).

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.mesh.Rectangle(a=(-1.2, 0.5), b=(4.5, 7.3), n=3)
>>> mesh.plot().show()
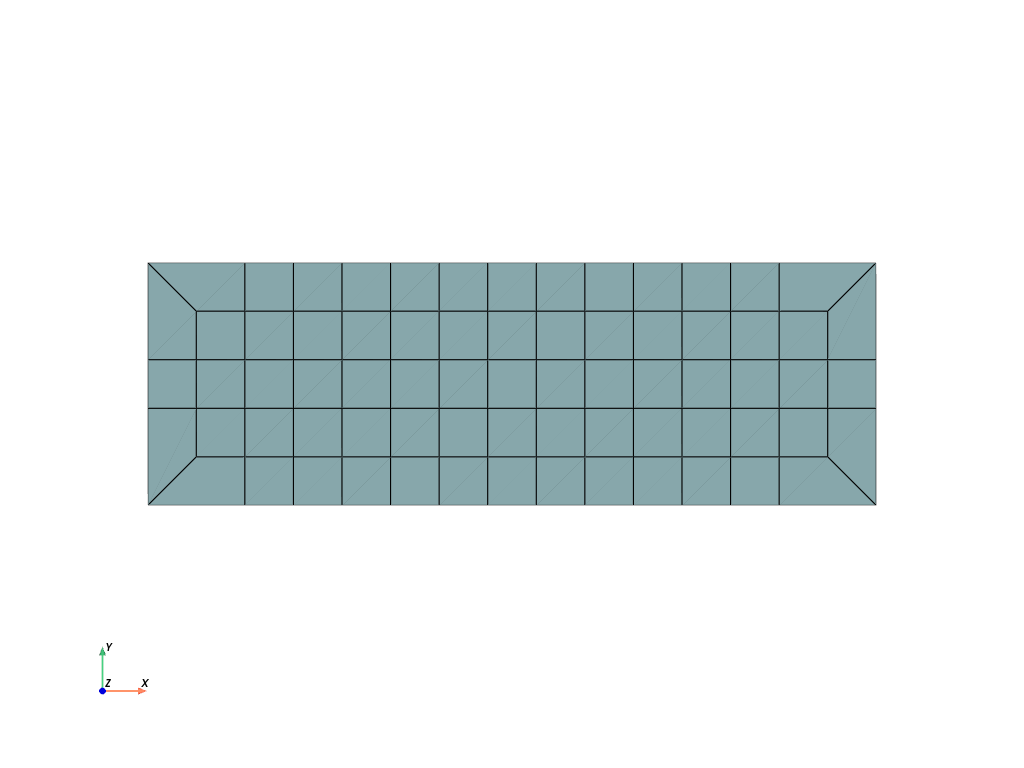
../_images/mesh-23_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 9
  Number of cells:
    quad: 4

>>> mesh.points
array([[-1.2 ,  0.5 ],
       [ 1.65,  0.5 ],
       [ 4.5 ,  0.5 ],
       [-1.2 ,  3.9 ],
       [ 1.65,  3.9 ],
       [ 4.5 ,  3.9 ],
       [-1.2 ,  7.3 ],
       [ 1.65,  7.3 ],
       [ 4.5 ,  7.3 ]])

>>> mesh.cells
array([[0, 1, 4, 3],
       [1, 2, 5, 4],
       [3, 4, 7, 6],
       [4, 5, 8, 7]])
class felupe.Cube(a=(0.0, 0.0, 0.0), b=(1.0, 1.0, 1.0), n=(2, 2, 2))[source]#

Bases: Mesh

A cube shaped 3d-mesh with hexahedrons between a and b with n points per axis.

Parameters:

  • a (3-tuple of float, optional) – Lower-left end point of the mesh (default is (0.0, 0.0, 0.0)).

  • b (3-tuple of float, optional) – Upper-right end point of the mesh (default is (1.0, 1.0, 1.0)).

  • n (int or 3-tuple of int, optional) – Number of points per axis (default is (2, 2, 2)).

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.mesh.Cube(a=(-1.2, 0.5, 6.2), b=(4.5, 7.3, 9.3), n=(3, 2, 2))
>>> mesh.plot().show()
../_images/mesh-24_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 12
  Number of cells:
    hexahedron: 2

>>> mesh.points
array([[-1.2 ,  0.5 ,  6.2 ],
       [ 1.65,  0.5 ,  6.2 ],
       [ 4.5 ,  0.5 ,  6.2 ],
       [-1.2 ,  7.3 ,  6.2 ],
       [ 1.65,  7.3 ,  6.2 ],
       [ 4.5 ,  7.3 ,  6.2 ],
       [-1.2 ,  0.5 ,  9.3 ],
       [ 1.65,  0.5 ,  9.3 ],
       [ 4.5 ,  0.5 ,  9.3 ],
       [-1.2 ,  7.3 ,  9.3 ],
       [ 1.65,  7.3 ,  9.3 ],
       [ 4.5 ,  7.3 ,  9.3 ]])

>>> mesh.cells
array([[ 0,  1,  4,  3,  6,  7, 10,  9],
       [ 1,  2,  5,  4,  7,  8, 11, 10]])
class felupe.Grid(*xi, indexing='ij', **kwargs)[source]#

Bases: Mesh

A grid shaped 3d-mesh with hexahedrons. Basically a wrapper for numpy.meshgrid() with default indexing="ij".

Parameters:

  • x1 (array_like) – 1-D arrays representing the coordinates of a grid.

  • x2 (array_like) – 1-D arrays representing the coordinates of a grid.

  • ... (array_like) – 1-D arrays representing the coordinates of a grid.

  • xn (array_like) – 1-D arrays representing the coordinates of a grid.

Examples

>>> import numpy as np
>>> import felupe as fem
>>>
>>> x1 = np.linspace(0, 2, 3)**2
>>> x2 = np.sqrt(np.linspace(0, 1, 3))
>>>
>>> mesh = fem.mesh.Grid(x1, x2)
>>> mesh.plot().show()
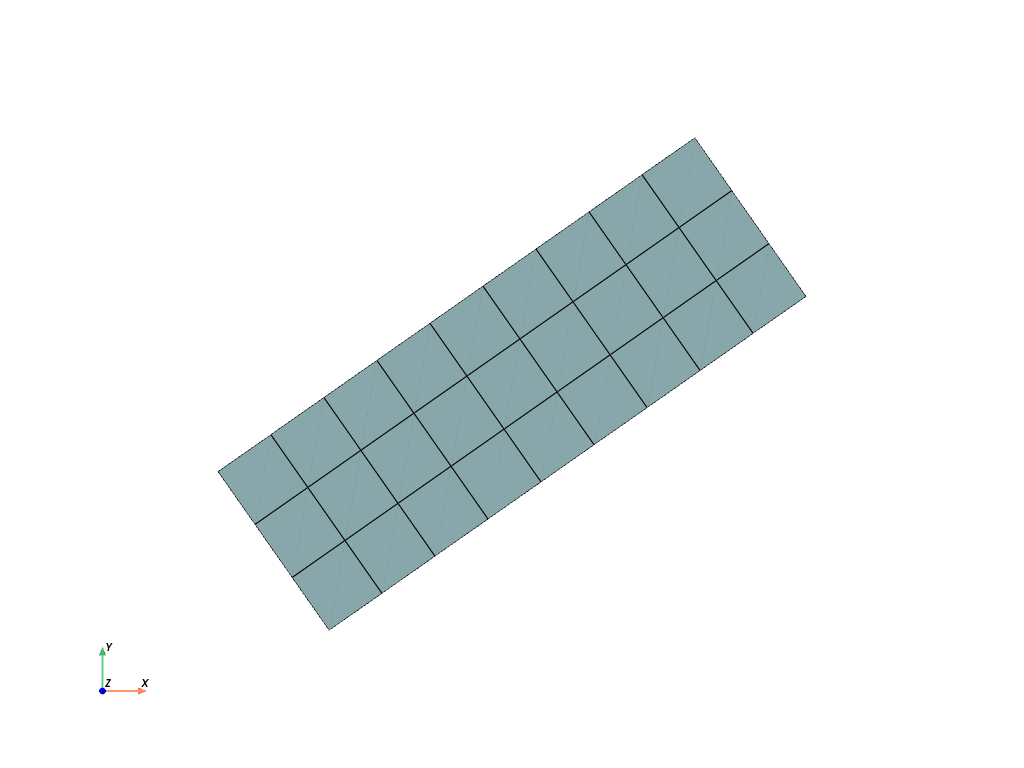
../_images/mesh-25_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 9
  Number of cells:
    quad: 4

>>> mesh.points
array([[0.        , 0.        ],
       [1.        , 0.        ],
       [4.        , 0.        ],
       [0.        , 0.70710678],
       [1.        , 0.70710678],
       [4.        , 0.70710678],
       [0.        , 1.        ],
       [1.        , 1.        ],
       [4.        , 1.        ]])

>>> mesh.cells
array([[0, 1, 4, 3],
       [1, 2, 5, 4],
       [3, 4, 7, 6],
       [4, 5, 8, 7]])

See also

numpy.meshgrid

Return a list of coordinate matrices from coordinate vectors.

class felupe.Circle(radius=1.0, centerpoint=[0.0, 0.0], n=2, sections=[0, 90, 180, 270], value=0.15, exponent=2, decimals=10)[source]#

Bases: Mesh

A circular shaped 2d-mesh with quads and n points on the circumferential edge of a 45-degree section. 90-degree sections are placed at given angles in degree.

Parameters:

  • radius (float, optional) – Lower-left end point of the mesh (default is (0.0, 0.0)).

  • centerpoint (2-list of float, optional) – Coordinates of the origin where the circle is centered (default is [1.0, 1.0]).

  • n (int, optional) – Number of points per axis for a quarter of the embedded rectangle (default is 2).

  • sections (list of int or float, optional) – Rotation angles in deg where quarter circles (sections) are placed (default is [0, 90, 180, 270]).

  • value (float) – First shape parameter of the embedded rectangle (default is 0.15).

  • exponent (int) – Second shape parameter of the embedded rectangle (default is 2).

  • decimals (int) – Decimals used for rounding point coordinates to avoid non-connected sections (default is 10).

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.mesh.Circle()
>>> mesh.plot().show()
../_images/mesh-26_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 17
  Number of cells:
    quad: 12

>>> mesh.points
array([[-1.        ,  0.        ],
       [-0.70710678, -0.70710678],
       [-0.70710678,  0.70710678],
       [-0.5       ,  0.        ],
       [-0.425     , -0.425     ],
       [-0.425     ,  0.425     ],
       [ 0.        , -1.        ],
       [ 0.        , -0.5       ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.5       ],
       [ 0.        ,  1.        ],
       [ 0.425     , -0.425     ],
       [ 0.425     ,  0.425     ],
       [ 0.5       ,  0.        ],
       [ 0.70710678, -0.70710678],
       [ 0.70710678,  0.70710678],
       [ 1.        ,  0.        ]])

>>> mesh.cells
array([[12, 13, 16, 15],
       [15, 10,  9, 12],
       [ 8, 13, 12,  9],
       [ 5,  9, 10,  2],
       [ 2,  0,  3,  5],
       [ 8,  9,  5,  3],
       [ 4,  3,  0,  1],
       [ 1,  6,  7,  4],
       [ 8,  3,  4,  7],
       [11,  7,  6, 14],
       [14, 16, 13, 11],
       [ 8,  7, 11, 13]])
class felupe.mesh.Triangle(a=(0.0, 0.0), b=(1.0, 0.0), c=(0.0, 1.0), n=2, decimals=10)[source]#

Bases: Mesh

A triangular shaped 2d-mesh with quads and n points at the edges of the three sub-quadrilaterals.

Parameters:

  • a (2-tuple of float, optional) – First end point of the mesh (default is (0.0, 0.0)).

  • b (2-tuple of float, optional) – Second end point of the mesh (default is (1.0, 0.0)).

  • c (2-tuple of float, optional) – Third end point of the mesh (default is (0.0, 1.0)).

  • n (int, optional) – Number of points per axis (default is 2).

  • decimals (int) – Decimals used for rounding point coordinates to avoid non-connected sections (default is 10).

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.mesh.Triangle(a=(0.3, 0.2), b=(1.2, 0.1), c=(0.1, 0.9), n=3)
>>> mesh.plot().show()
../_images/mesh-27_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 19
  Number of cells:
    quad: 12

>>> mesh.points
array([[0.1       , 0.9       ],
       [0.15      , 0.725     ],
       [0.2       , 0.55      ],
       [0.25      , 0.375     ],
       [0.3       , 0.2       ],
       [0.36666667, 0.475     ],
       [0.37083333, 0.5875    ],
       [0.375     , 0.7       ],
       [0.44583333, 0.325     ],
       [0.525     , 0.175     ],
       [0.53333333, 0.4       ],
       [0.59166667, 0.45      ],
       [0.64166667, 0.275     ],
       [0.65      , 0.5       ],
       [0.75      , 0.15      ],
       [0.78333333, 0.2875    ],
       [0.925     , 0.3       ],
       [0.975     , 0.125     ],
       [1.2       , 0.1       ]])

>>> mesh.cells
array([[14, 12,  8,  9],
       [12, 10,  5,  8],
       [ 9,  8,  3,  4],
       [ 8,  5,  2,  3],
       [18, 16, 15, 17],
       [16, 13, 11, 15],
       [17, 15, 12, 14],
       [15, 11, 10, 12],
       [10, 11,  6,  5],
       [11, 13,  7,  6],
       [ 5,  6,  1,  2],
       [ 6,  7,  0,  1]])
class felupe.mesh.RectangleArbitraryOrderQuad(a=(0.0, 0.0), b=(1.0, 1.0), order=2)[source]#

Bases: Rectangle

A rectangular 2d-mesh with an arbitrarr-order Lagrange quad between a and b.

class felupe.mesh.CubeArbitraryOrderHexahedron(a=(0.0, 0.0, 0.0), b=(1.0, 1.0, 1.0), order=2)[source]#

Bases: Cube

A rectangular 2d-mesh with an arbitrarr-order Lagrange hexahedron between a and b.

felupe.mesh.add_midpoints_edges(points, cells, cell_type, cell_type_new=None)[source]#

Add midpoints on edges for given points and cells and update cell_type accordingly.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • cell_type_new (str or None, optional) – A string in VTK-convention that specifies the new cell type (default is None). If None, the cell type is chosen automatically.

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

Convert a mesh of hexahedrons to quadratic hexahedrons by inserting midpoints on the cell edges.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=6)
>>> mesh_with_midpoints_edges = fem.mesh.add_midpoints_edges(mesh)
>>>
>>> plotter = mesh_with_midpoints_edges.plot(
...     plotter=mesh.plot(), style="points", color="black"
... )
>>> plotter.show()

>>> mesh_with_midpoints_edges
<felupe Mesh object>
  Number of points: 96
  Number of cells:
    quad8: 25

See also

felupe.Mesh.add_midpoints_edges

Add midpoints on edges for given points and cells and update cell_type accordingly.

felupe.mesh.add_midpoints_faces(points, cells, cell_type, cell_type_new=None)[source]#

Add midpoints on faces for given points and cells and update cell_type accordingly.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • cell_type_new (str or None, optional) – A string in VTK-convention that specifies the new cell type (default is None). If None, the cell type is chosen automatically.

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=6)
>>> mesh_with_midpoints_faces = fem.mesh.add_midpoints_faces(
...     mesh, cell_type_new="quad"
... )
>>>
>>> plotter = mesh_with_midpoints_faces.plot(
...     plotter=mesh.plot(), style="points", color="black"
... )
>>> plotter.show()

>>> mesh_with_midpoints_faces
<felupe Mesh object>
  Number of points: 61
  Number of cells:
    quad: 25

See also

felupe.Mesh.add_midpoints_faces

Add midpoints on faces for given points and cells and update cell_type accordingly.

felupe.mesh.add_midpoints_volumes(points, cells, cell_type, cell_type_new=None)[source]#

Add midpoints on volumes for given points and cells and update cell_type accordingly.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • cell_type_new (str or None, optional) – A string in VTK-convention that specifies the new cell type (default is None). If None, the cell type is chosen automatically.

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=6)
>>> mesh_with_midpoints_volumes = fem.mesh.add_midpoints_volumes(
...     mesh, cell_type_new="hexahedron9"
... )
>>>
>>> plotter = mesh.plot(opacity=0.5)
>>> actor = plotter.add_points(mesh_with_midpoints_volumes.points, color="black")
>>> plotter.show()

>>> mesh_with_midpoints_volumes
<felupe Mesh object>
  Number of points: 341
  Number of cells:
    hexahedron9: 125

See also

felupe.Mesh.add_midpoints_volumes

Add midpoints on volumes for given points and cells and update cell_type accordingly.

felupe.mesh.collect_edges(points, cells, cell_type)[source]#

Collect all unique edges, calculate and return midpoints on edges as well as the additional cells array.

See also

felupe.mesh.add_midpoints_edges

Add midpoints on cell edges for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_edges

Add midpoints on cell edges for given points and cells and update cell_type accordingly.

felupe.mesh.collect_faces(points, cells, cell_type)[source]#

Collect all unique faces, calculate and return midpoints on faces as well as the additional cells array.

See also

felupe.mesh.add_midpoints_faces

Add midpoints on cell faces for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_faces

Add midpoints on cell faces for given points and cells and update cell_type accordingly.

felupe.mesh.collect_volumes(points, cells, cell_type)[source]#

Collect all volumes, calculate and return midpoints on volumes as well as the additional cells array.

See also

felupe.mesh.add_midpoints_volumes

Add midpoints on cell volumes for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_volumes

Add midpoints on cell volumes for given points and cells and update cell_type accordingly.

felupe.mesh.concatenate(meshes)[source]#

Join a sequence of meshes with identical cell types.

Parameters:

meshes (list of Mesh) – A list with meshes.

Returns:

The joined mesh.

Return type:

Mesh

Notes

The points-arrays are vertically stacked. Offsets are added to the cells- arrays of the meshes to refer to the original points.

Examples

Two quad meshes should be joined (merged) into a single mesh.

>>> import felupe as fem
>>>
>>> rect1 = fem.Rectangle(n=11)
>>> rect2 = fem.Rectangle(a=(0.9, 0), b=(1.9, 1), n=11)
>>>
>>> mesh = fem.mesh.concatenate([rect1, rect2])
>>> mesh.plot(opacity=0.6).show()

Each mesh contains 121 points and 100 cells.

>>> rect1
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

>>> rect2
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

These two meshes are stored in a Mesh. Note that there are duplicate points and cells in the joined mesh.

>>> mesh
<felupe Mesh object>
  Number of points: 242
  Number of cells:
    quad: 200
felupe.mesh.convert(points, cells, cell_type, order=0, calc_points=False, calc_midfaces=False, calc_midvolumes=False)[source]#

Convert a mesh to a given order. Only conversions to order=0 and order=2 are supported. This function supports meshes with cell types "triangle", "tetra", "quad" and "hexahedron".

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type. Must be one of "triangle", "tetra", "quad" or "hexahedron".

  • order (int, optional) – The order of the converted mesh (default is 0). If 0, the points-array will be of shape (ncells, dim). If 0 and calc_points is True, the mean of all points per cell is evaluated. If 0 and calc_points is False, the points array is filled with zeros. If 2, at least midpoints on cell edges are added to the mesh. If 2 and calc_midfaces is True, midpoints on cell faces are also added. If 2 and calc_midvolumes is True, midpoints on cell volumes are also added. Raises an error if not 0 or 2.

  • calc_points (bool, optional) – Flag to return the mean of all points per cell if order=0 (default is False). If False, the points-array is filled with zeros.

  • calc_midfaces (bool, optional) – Flag to add midpoints on cell faces if order=2 (default is False).

  • calc_midvolumes (bool, optional) – Flag to add midpoints on cell volumes if order=2 (default is False).

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (list or ndarray) – Converted cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

Convert a mesh of hexahedrons to quadratic hexahedrons by inserting midpoints on the cell edges.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=6)
>>> mesh2 = fem.mesh.convert(mesh, order=2)
>>>
>>> plotter = mesh2.plot(plotter=mesh.plot(), style="points", color="black")
>>> plotter.show()

>>> mesh2
<felupe Mesh object>
  Number of points: 96
  Number of cells:
    quad8: 25

See also

felupe.mesh.add_midpoints_edges

Add midpoints on edges for given points and cells and update cell_type accordingly.

felupe.mesh.add_midpoints_faces

Add midpoints on faces for given points and cells and update cell_type accordingly.

felupe.mesh.add_midpoints_volumes

Add midpoints on volumes for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_edges

Add midpoints on edges for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_faces

Add midpoints on faces for given points and cells and update cell_type accordingly.

felupe.Mesh.add_midpoints_volumes

Add midpoints on volumes for given points and cells and update cell_type accordingly.

felupe.mesh.dual(points, cells, cell_type, points_per_cell=None, disconnect=True, calc_points=False, offset=0, npoints=None)[source]#

Create a new dual mesh with given points per cell.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • points_per_cell (int or None, optional) – Number of points per cell, must be equal or lower than cells.shape[1] ( default is None). If None, all points per cell are considered for the dual mesh.

  • disconnect (bool, optional) – A flag to disconnect the mesh (each cell has its own points). Default is True.

  • calc_points (bool, optional) – A flag to calculate the point coordinates for the dual mesh (default is False). If False, the points array is filled with zeros.

  • offset (int, optional) – An offset to be added to the cells array (default is 0).

  • npoints (int or None, optional) – Number of points for the dual mesh. If the given number of points is greater than npoints * points_per_cell, then the missing points are added to the points array (filled with zeros). Default is None.

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (list or ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Notes

Note

The points array of the dual mesh always has a shape of (npoints * points_per_cell, dim).

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=5).add_midpoints_edges()
>>> region = fem.RegionQuadraticQuad(mesh=mesh)
>>>
>>> mesh_dual = fem.mesh.dual(mesh, points_per_cell=1, disconnect=False)
>>> region_dual = fem.RegionConstantQuad(
...     mesh_dual, quadrature=region.quadrature, grad=False
... )
>>>
>>> displacement = fem.FieldPlaneStrain(region, dim=2)
>>> pressure = fem.Field(region_dual)
>>> field = fem.FieldContainer([displacement, pressure])

See also

felupe.Mesh.dual

Create a new dual mesh with given points per cell.

felupe.mesh.expand(points, cells, cell_type, n=11, z=1, axis=-1, expand_dim=True)[source]#

Expand a 0d-Point to a 1d-Line, a 1d-Line to a 2d-Quad or a 2d-Quad to a 3d-Hexahedron Mesh.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • n (int, optional) – Number of n-point repetitions or (n-1)-cell repetitions, default is 11. Must be greater or equal 0.

  • z (float or ndarray, optional) – Total expansion as float (edge length in expand direction is z / (n - 1)), default is 1. Optionally, if an array is passed these entries are taken as expansion and n is ignored.

  • axis (int, optional) – Axis of expansion (default is -1).

  • expand_dim (bool, optional) – Expand the dimension of the point coordinates (default is True).

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

Expand a rectangle to a cube.

>>> import felupe as fem
>>>
>>> rect = fem.Rectangle(n=4)
>>> cube = fem.mesh.expand(rect, n=7, z=2)
>>>
>>> cube.plot().show()
../_images/mesh-32_00_00.png 
>>> cube
<felupe Mesh object>
  Number of points: 112
  Number of cells:
    hexahedron: 54

See also

felupe.Mesh.expand

Expand a 0d-Point to a 1d-Line, a 1d-Line to a 2d-Quad or a 2d-Quad to a 3d-Hexahedron Mesh.

felupe.mesh.fill_between(mesh, other_mesh, n=11)[source]#

Fill a 2d-Quad Mesh between two 1d-Line Meshes, embedded in 2d-space, or a 3d-Hexahedron Mesh between two 2d-Quad Meshes, embedded in 3d-space, by expansion. Both meshes must have equal number of points and cells. The cells-array is taken from the first mesh.

Parameters:

  • mesh (felupe.Mesh) – The base line- or quad-mesh.

  • other_mesh (felupe.Mesh) – The other line- or quad-mesh.

  • n (int or ndarray) – Number of n-point repetitions or (n-1)-cell repetitions, (default is 11). If an array is given, then its values are used for the relative positions in a reference configuration (-1, 1) between the two meshes.

Returns:

mesh – The expanded mesh.

Return type:

felupe.Mesh

Examples

>>> import felupe as fem
>>>
>>> inner = fem.mesh.revolve(fem.Point(1)).expand(z=0.4).translate(0.2, axis=2)
>>> outer = fem.mesh.revolve(fem.Point(2), phi=160).rotate(
...     axis=2, angle_deg=20
... ).expand(z=1.2)
>>> mesh = fem.mesh.fill_between(inner, outer, n=6)
>>>
>>> mesh.plot().show()
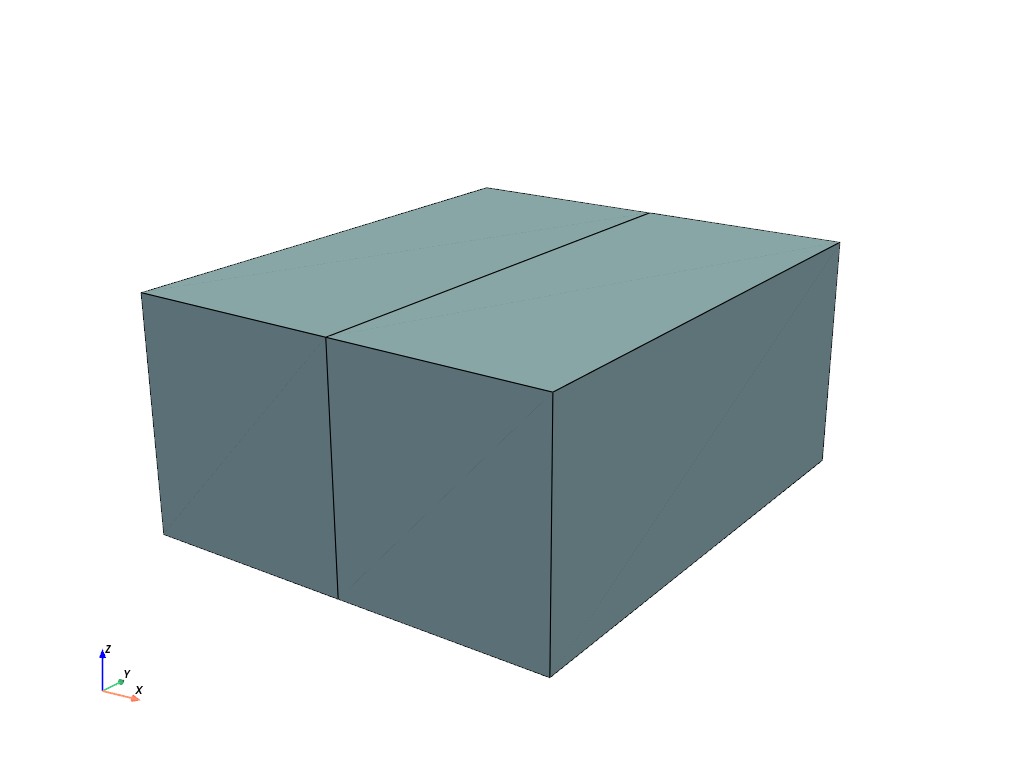
../_images/mesh-33_00_00.png

See also

felupe.Mesh.fill_between

Fill a 2d-Quad Mesh between two 1d-Line Meshes, embedded in 2d-space, or a 3d-Hexahedron Mesh between two 2d-Quad Meshes, embedded in 3d-space, by expansion.

felupe.mesh.flip(points, cells, cell_type, mask=None)[source]#

Ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • mask (list, ndarray or None, optional) – Boolean mask for selected cells to flip (default is None). If None, all cells are selected to be flipped.

Returns:

  • points (ndarray) – Point coordinates.

  • cells (ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

A quad mesh with negative cell volumes occurs if one coordinate axis is multiplied by -1. The error pops up if a region is created with this mesh.

>>> import numpy as np
>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=3)
>>> mesh.update(points=mesh.points * np.array([[-1, 1]]))
>>> region = fem.RegionQuad(mesh)

The sum of the differential volumes \(V = \sum_c \sum_q dV_{qc}\) is evaluated to -1.0.

>>> region.dV.sum()
-1.0

Let’s try to fix the mesh.

>>> mesh.cells
array([[0, 1, 4, 3],
       [1, 2, 5, 4],
       [3, 4, 7, 6],
       [4, 5, 8, 7]])

The cells array is rearranged to ensure positive cell volumes.

>>> mesh_fixed = fem.mesh.flip(mesh)
>>> mesh_fixed.cells
array([[3, 4, 1, 0],
       [4, 5, 2, 1],
       [6, 7, 4, 3],
       [7, 8, 5, 4]])

A region now correctly evaluates the total volume of the mesh to 1.0.

>>> region_fixed = fem.RegionQuad(mesh_fixed)
>>> region_fixed.dV.sum()
1.0

See also

felupe.Mesh.flip

Ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

felupe.mesh.merge_duplicate_cells(points, cells, cell_type)[source]#

Merge duplicate cells of a Mesh.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

Returns:

  • points (ndarray) – Point coordinates.

  • cells (list or ndarray) – Cells with merged duplicate cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Notes

Warning

This function re-sorts cells.

Note

This function does not merge duplicate points.

Examples

Two quad meshes to be merged overlap some cells. Merge these duplicated points and update the cells.

>>> import felupe as fem
>>>
>>> rect1 = fem.Rectangle(n=11)
>>> rect2 = fem.Rectangle(a=(0.9, 0), b=(1.9, 1), n=11)
>>>
>>> container = fem.MeshContainer([rect1, rect2])
>>> stack = fem.mesh.stack(container.meshes)
>>> mesh = fem.mesh.merge_duplicate_points(stack)
>>>
>>> mesh.plot(opacity=0.6).show()
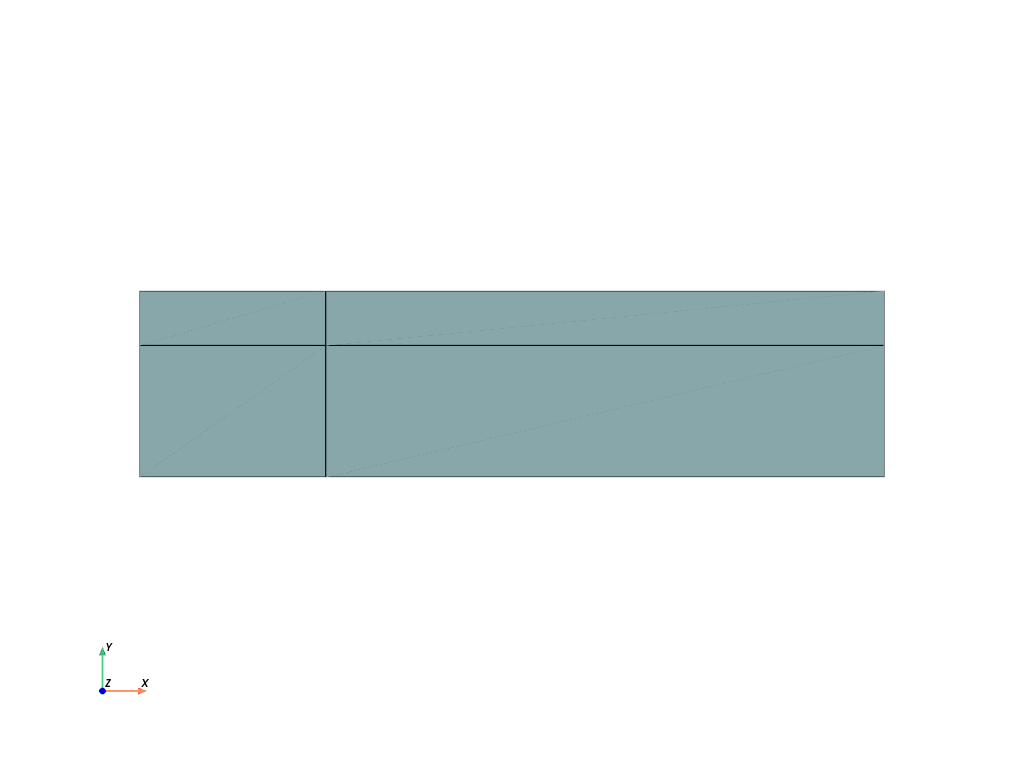
../_images/mesh-34_00_00.png

Each mesh contains 121 points and 100 cells.

>>> rect1
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

>>> rect2
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

These two meshes are now stored in a MeshContainer.

>>> container
<felupe mesh container object>
  Number of points: 242
  Number of cells:
    quad: 100
    quad: 100

The meshes of the mesh container are stacked.

>>> stack
<felupe Mesh object>
  Number of points: 242
  Number of cells:
    quad: 200

After merging the duplicated points and cells, the number of points is reduced but the number of cells is unchanged.

>>> mesh
<felupe Mesh object>
  Number of points: 220
  Number of cells:
    quad: 200

Note

The MeshContainer may be directly created with merge=True. This enforces merge_duplicate_points() for the shared points array of the container.

The duplicate cells are merged in a second step.

>>> merged = fem.mesh.merge_duplicate_cells(mesh)
>>> merged
<felupe Mesh object>
  Number of points: 220
  Number of cells:
    quad: 190
felupe/images/mesh_merged.png

See also

felupe.Mesh.merge_duplicate_points

Merge duplicate points of a Mesh.

felupe.Mesh.merge_duplicate_cells

Merge duplicate cells of a Mesh.

felupe.MeshContainer

A container which operates on a list of meshes with identical dimensions.

felupe.mesh.merge_duplicate_points(points, cells, cell_type, decimals=None)[source]#

Merge duplicate points and update cells of a Mesh.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • decimals (int or None, optional) – Number of decimals for point coordinate comparison (default is None).

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (list or ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Notes

Warning

This function re-sorts points.

Note

This function does not merge duplicate cells.

Examples

Two quad meshes to be merged overlap some points. Merge these duplicated points and update the cells. .. pyvista-plot:

:include-source: True

>>> import felupe as fem
>>>
>>> rect1 = fem.Rectangle(n=11)
>>> rect2 = fem.Rectangle(a=(0.9, 0), b=(1.9, 1), n=11)
>>>
>>> container = fem.MeshContainer([rect1, rect2])
>>> stack = fem.mesh.stack(container.meshes)
>>> mesh = fem.mesh.merge_duplicate_points(stack)
>>>
>>> mesh.plot(opacity=0.6).show()

Each mesh contains 121 points and 100 cells.

>>> rect1
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

>>> rect2
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

These two meshes are now stored in a MeshContainer.

>>> container
<felupe mesh container object>
  Number of points: 242
  Number of cells:
    quad: 100
    quad: 100

The meshes of the mesh container are stacked.

>>> stack
<felupe Mesh object>
  Number of points: 242
  Number of cells:
    quad: 200

After merging the duplicated points and cells, the number of points is reduced but the number of cells is unchanged.

>>> mesh
<felupe Mesh object>
  Number of points: 220
  Number of cells:
    quad: 200

Note

The MeshContainer may be directly created with merge=True. This enforces merge_duplicate_points() for the shared points array of the container.

See also

felupe.Mesh.merge_duplicate_points

Merge duplicated points and update cells of a Mesh.

felupe.MeshContainer

A container which operates on a list of meshes with identical dimensions.

felupe.mesh.mirror(points, cells, cell_type, normal=[1, 0, 0], centerpoint=[0, 0, 0], axis=None)[source]#

Mirror points by plane normal and ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • normal (list or ndarray, optional) – Mirror-plane normal vector (default is [1, 0, 0]).

  • centerpoint (list or ndarray, optional) – Center-point coordinates on the mirror plane (default is [0, 0, 0]).

  • axis (int or None, optional) – Mirror axis (default is None).

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Circle(sections=[0, 90, 180], n=5)
>>> mesh.plot().show()
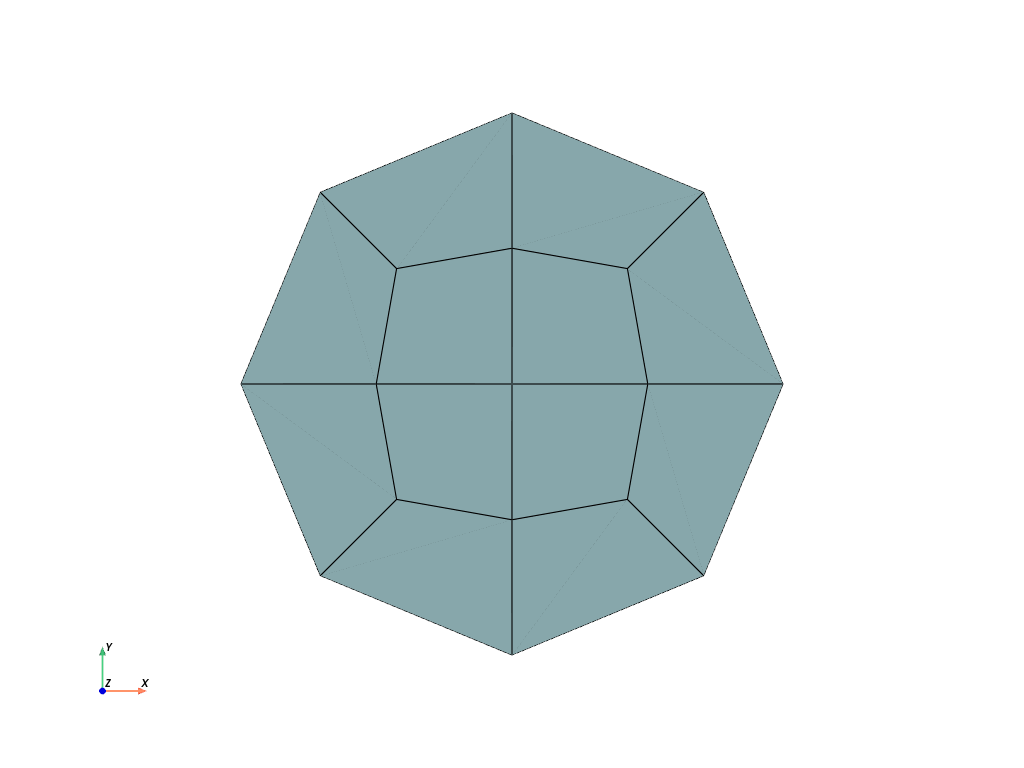
../_images/mesh-35_00_00.png 
>>> import felupe as fem
>>>
>>> mesh = fem.Circle(sections=[0, 90, 180], n=5)
>>> fem.mesh.mirror(mesh, normal=[0, 1, 0]).plot().show()
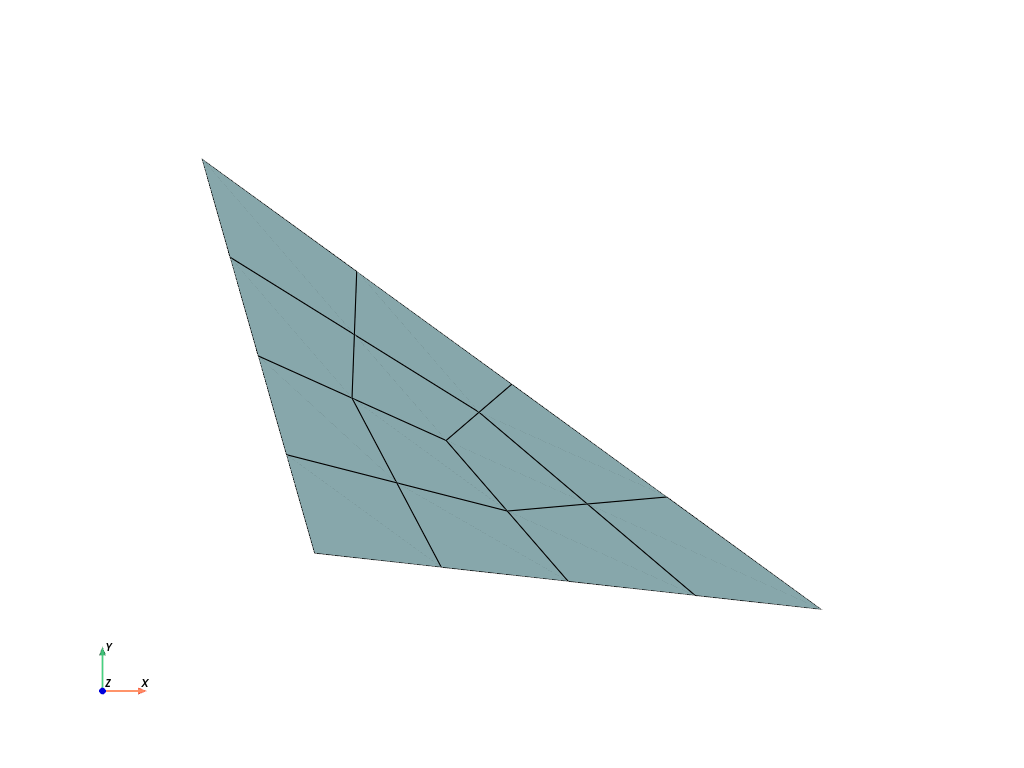
../_images/mesh-36_00_00.png

See also

felupe.Mesh.mirror

Mirror points by plane normal and ensure positive cell volumes for tria, tetra, quad and hexahedron cell types.

felupe.mesh.read(filename, file_format=None, cellblock=None, dim=None, merge=False, decimals=None)[source]#

Read a mesh from a file using meshio.read() and create a MeshContainer.

Parameters:

  • filename (str) – The filename of the mesh file.

  • file_format (str or None, optional) – The file format of the mesh file (default is None).

  • cellblock (list of int or None, optional) – Read only a subset of the cellblocks from the mesh file (default is None). If None, all cell blocks are added to the MeshContainer.

  • dim (int or None, optional) – If provided, the dimension to trim the points array to (default is None). If None, the points array is unchanged.

  • merge (bool, optional) – Flag to merge duplicate mesh points. This changes the cells arrays of the meshes. Default is False.

  • decimals (float or None, optional) – Precision decimals for merging duplicated mesh points. Only relevant if merge=True. Default is None.

Returns:

A mesh container created with meshio.read().

Return type:

MeshContainer

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=3)
>>> mesh.write(filename="mesh.xdmf")

>>> container = fem.mesh.read("mesh.xdmf")
>>> container
<felupe mesh container object>
  Number of points: 9
  Number of cells:
    quad: 4

>>> container.meshes[0]
<felupe Mesh object>
  Number of points: 9
  Number of cells:
    quad: 4

See also

meshio.read

Reads an unstructured mesh with added data.

felupe.Mesh.write

Write the mesh to a file.

felupe.mesh.revolve(points, cells, cell_type, n=11, phi=180, axis=0, expand_dim=True)[source]#

Revolve a 0d-Point to a 1d-Line, a 1d-Line to 2d-Quad or a 2d-Quad to a 3d-Hexahedron Mesh.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • n (int, optional) – Number of n-point revolutions (or (n-1) cell revolutions), default is 11.

  • phi (float or ndarray, optional) – Revolution angle in degree (default is 180).

  • axis (int, optional) – Revolution axis (default is 0).

  • expand_dim (bool, optional) – Expand the dimension of the point coordinates (default is True).

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (list or ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

Revolve a cylinder from a rectangle.

>>> import felupe as fem
>>>
>>> rect = fem.Rectangle(a=(0, 4), b=(3, 5), n=(10, 4))
>>> mesh = fem.mesh.revolve(rect, n=11, phi=180, axis=0)
>>> mesh.plot().show()
../_images/mesh-37_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 440
  Number of cells:
    hexahedron: 270

See also

felupe.Mesh.revolve

Revolve a 2d-Quad to a 3d-Hexahedron Mesh.

felupe.mesh.rotate(points, cells, cell_type, angle_deg, axis, center=None, mask=None)[source]#

Rotate a Mesh.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • angle_deg (int) – Rotation angle in degree.

  • axis (int) – Rotation axis.

  • center (list or ndarray or None, optional) – Center point coordinates (default is None).

  • mask (ndarray or None, optional) – A boolean mask to select points which are rotated (default is None).

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

Rotate a rectangle in the xy-plane by 35 degree.

>>> import felupe as fem
>>>
>>> rect = fem.Rectangle(b=(3, 1), n=(10, 4))
>>> mesh = fem.mesh.rotate(rect, angle_deg=35, axis=2, center=[1.5, 0.5])
>>> mesh.plot().show()
../_images/mesh-38_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 40
  Number of cells:
    quad: 27

See also

felupe.Mesh.rotate

Rotate a Mesh.

felupe.mesh.runouts(points, cells, cell_type, values=[0.1, 0.1], centerpoint=[0, 0, 0], axis=0, exponent=5, mask=slice(None, None, None), normalize=False)[source]#

Add simple rubber-runouts for realistic rubber-metal structures.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • values (list or ndarray, optional) – Relative amount of runouts (per coordinate) perpendicular to the axis (default is 10% per coordinate, i.e. [0.1, 0.1]).

  • centerpoint (list or ndarray, optional) – Center-point coordinates (default is [0, 0, 0]).

  • axis (int or None, optional) – Axis (default is 0).

  • exponent (int, optional) – Positive exponent to control the shape of the runout. The higher the exponent, the steeper the transition (default is 5).

  • mask (list or None, optional) – List of points to be considered (default is None).

  • normalize (bool, optional) – Normalize the runouts to create indents, i.e. maintain the original shape at the ends (default is False).

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

>>> import felupe as fem
>>>
>>> rect = fem.Rectangle(a=(-3, -1), b=(3, 1), n=(31, 11))
>>> mesh = fem.mesh.runouts(rect, axis=1, values=[0.2], normalize=True)
>>>
>>> mesh.plot().show()
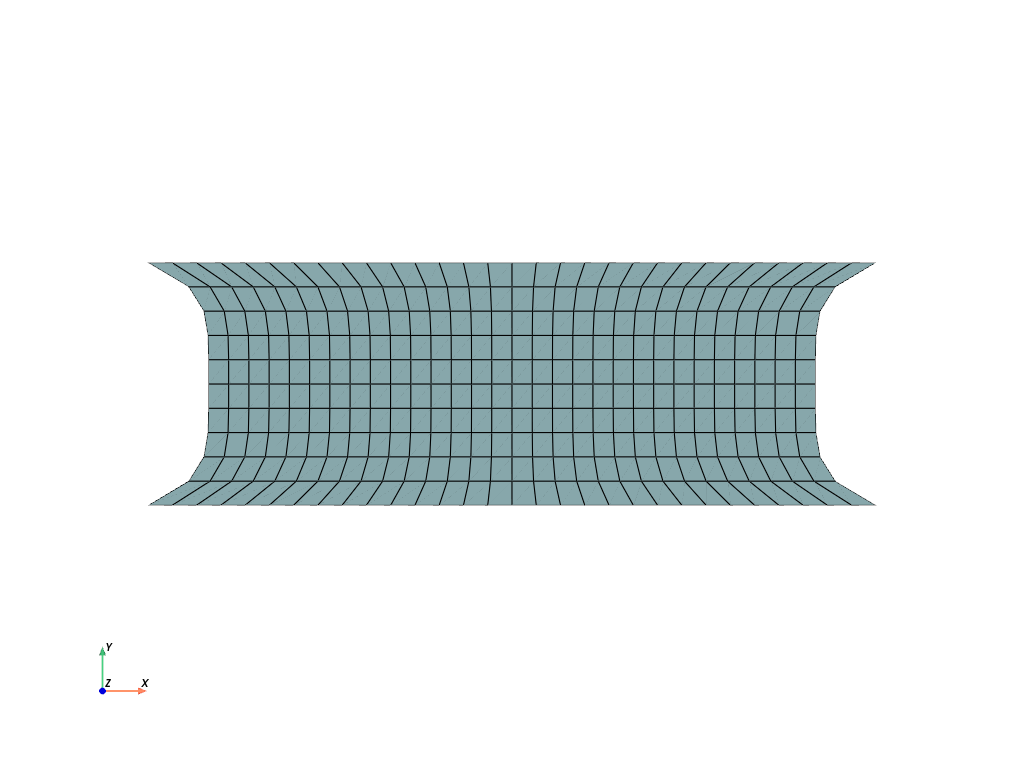
../_images/mesh-39_00_00.png 
>>> import felupe as fem
>>>
>>> cube = fem.Cube(a=(-3, -2, -1), b=(3, 2, 1), n=(31, 21, 11))
>>> mesh = fem.mesh.runouts(cube, axis=2, values=[0.1, 0.3], normalize=True)
>>>
>>> mesh.plot().show()
../_images/mesh-40_00_00.png

See also

felupe.Mesh.add_runouts

Add simple rubber-runouts for realistic rubber-metal structures.

felupe.mesh.stack(meshes)[source]#

Stack cell-blocks from meshes with identical points-array and cell-types.

Parameters:

meshes (list of Mesh) – A list with meshes. The points-array is taken from the first mesh in the list.

Returns:

The stacked mesh.

Return type:

Mesh

Notes

The points-array is taken from the first mesh. The points-arrays of all meshes must be identical. The cells-array of the stacked mesh is created by a vertical stack of the cells-arrays.

Examples

Two quad meshes with identical point arrays should be stacked into a single mesh.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle(n=11)
>>> rect1, rect2 = mesh.copy(), mesh.copy()
>>> rect1.update(cells=mesh.cells[: 40])
>>> rect2.update(cells=mesh.cells[-50:])
>>>
>>> mesh = fem.mesh.stack([rect1, rect2])
>>> mesh.plot().show()
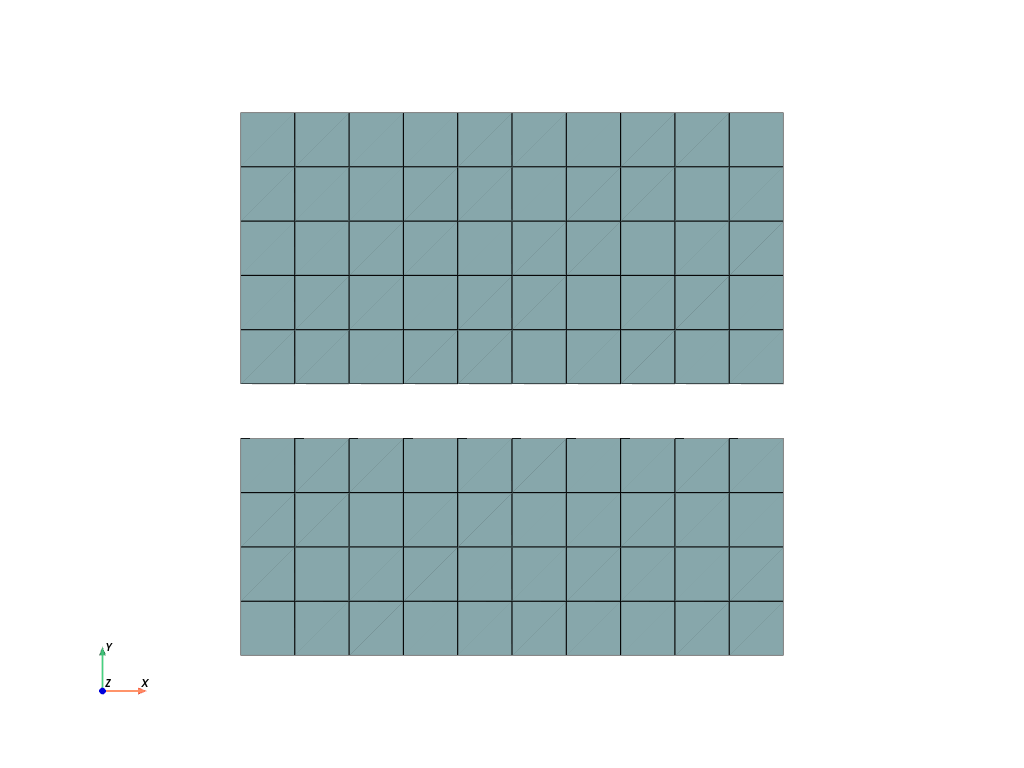
../_images/mesh-41_00_00.png 
>>> mesh
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 90

See also

felupe.MeshContainer.stack

Stack cell-blocks with same cell-types into a single mesh.

felupe.mesh.sweep(points, cells, cell_type, decimals=None)#

Merge duplicate points and update cells of a Mesh.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • decimals (int or None, optional) – Number of decimals for point coordinate comparison (default is None).

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (list or ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Notes

Warning

This function re-sorts points.

Note

This function does not merge duplicate cells.

Examples

Two quad meshes to be merged overlap some points. Merge these duplicated points and update the cells. .. pyvista-plot:

:include-source: True

>>> import felupe as fem
>>>
>>> rect1 = fem.Rectangle(n=11)
>>> rect2 = fem.Rectangle(a=(0.9, 0), b=(1.9, 1), n=11)
>>>
>>> container = fem.MeshContainer([rect1, rect2])
>>> stack = fem.mesh.stack(container.meshes)
>>> mesh = fem.mesh.merge_duplicate_points(stack)
>>>
>>> mesh.plot(opacity=0.6).show()

Each mesh contains 121 points and 100 cells.

>>> rect1
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

>>> rect2
<felupe Mesh object>
  Number of points: 121
  Number of cells:
    quad: 100

These two meshes are now stored in a MeshContainer.

>>> container
<felupe mesh container object>
  Number of points: 242
  Number of cells:
    quad: 100
    quad: 100

The meshes of the mesh container are stacked.

>>> stack
<felupe Mesh object>
  Number of points: 242
  Number of cells:
    quad: 200

After merging the duplicated points and cells, the number of points is reduced but the number of cells is unchanged.

>>> mesh
<felupe Mesh object>
  Number of points: 220
  Number of cells:
    quad: 200

Note

The MeshContainer may be directly created with merge=True. This enforces merge_duplicate_points() for the shared points array of the container.

See also

felupe.Mesh.merge_duplicate_points

Merge duplicated points and update cells of a Mesh.

felupe.MeshContainer

A container which operates on a list of meshes with identical dimensions.

felupe.mesh.translate(points, cells, cell_type, move, axis)[source]#

Translate (move) a Mesh along a given axis.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • move (float) – Translation along given axis.

  • axis (int) – Translation axis.

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

>>> import felupe as fem
>>>
>>> mesh = fem.Circle(n=6)
>>> mesh.points.min(axis=0), mesh.points.max(axis=0)
(array([-1., -1.]), array([1., 1.]))

>>> translated = fem.mesh.translate(mesh, 0.3, axis=1)
>>> translated.points.min(axis=0), translated.points.max(axis=0)
(array([-1. , -0.7]), array([1. , 1.3]))

See also

felupe.Mesh.translate

Translate (move) a Mesh along a given axis.

felupe.mesh.triangulate(points, cells, cell_type, mode=3)[source]#

Triangulate a quad or a hex mesh.

Parameters:

  • points (list or ndarray) – Original point coordinates.

  • cells (list or ndarray) – Original point-connectivity of cells.

  • cell_type (str) – A string in VTK-convention that specifies the cell type.

  • mode (int, optional) – Choose a mode how to convert hexahedrons to tets [1]_ (default is 3).

Returns:

  • points (ndarray) – Modified point coordinates.

  • cells (ndarray) – Modified point-connectivity of cells.

  • cell_type (str or None) – A string in VTK-convention that specifies the cell type.

Examples

Use mode=0 to convert a mesh of hexahedrons into tetrahedrons [1]_.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=6)
>>> triangulated = fem.mesh.triangulate(mesh, mode=0)
>>> triangulated.plot().show()
../_images/mesh-42_00_00.png

Use mode=3 to convert a mesh of hexahedrons into tetrahedrons [1]_.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=6)
>>> triangulated = fem.mesh.triangulate(mesh, mode=3)
>>> triangulated.plot().show()
../_images/mesh-43_00_00.png

References

See also

felupe.Mesh.triangulate

Triangulate a quad or a hex mesh.

On this page
Show Source