Ctrl+K

Region#

This module contains the definition of a region as well as a boundary region along with template-regions for pre-defined combinations of elements and quadrature rules.

Core

Region(mesh, element, quadrature[, grad])

A numeric region as a combination of a mesh, an element and a numeric integration scheme (quadrature rule).

RegionBoundary(mesh, element, quadrature[, ...])

A numeric boundary-region as a combination of a mesh, an element and a numeric integration scheme (quadrature rule).

Templates

RegionQuad(mesh[, quadrature, grad])

A region with a quad element.

RegionHexahedron(mesh[, quadrature, grad])

A region with a hexahedron element.

RegionTriangle(mesh[, quadrature, grad])

A region with a triangle element.

RegionTetra(mesh[, quadrature, grad])

A region with a tetra element.

RegionConstantQuad(mesh[, quadrature, grad])

A region with a constant quad element.

RegionConstantHexahedron(mesh[, quadrature, ...])

A region with a constant hexahedron element.

RegionQuadraticQuad(mesh[, quadrature, grad])

A region with a (serendipity) quadratic quad element.

RegionQuadraticHexahedron(mesh[, ...])

A region with a (serendipity) quadratic hexahedron element.

RegionQuadraticTriangle(mesh[, quadrature, grad])

A region with a quadratic triangle element.

RegionQuadraticTetra(mesh[, quadrature, grad])

A region with a quadratic tetra element.

RegionBiQuadraticQuad(mesh[, quadrature, grad])

A region with a bi-quadratic (Lagrange) quad element.

RegionTriQuadraticHexahedron(mesh[, ...])

A region with a tri-quadratic (Lagrange) hexahedron element.

RegionTriangleMINI(mesh[, quadrature, grad, ...])

A region with a triangle-MINI element.

RegionTetraMINI(mesh[, quadrature, grad, ...])

A region with a tetra-MINI element.

RegionLagrange(mesh, order, dim[, ...])

A region with an arbitrary order Lagrange element.

RegionQuadBoundary(mesh[, quadrature, grad, ...])

A region with a quad element.

RegionHexahedronBoundary(mesh[, quadrature, ...])

A boundary region with a hexahedron element.

Detailed API Reference

class felupe.Region(mesh, element, quadrature, grad=True)[source]#

A numeric region as a combination of a mesh, an element and a numeric integration scheme (quadrature rule).

Parameters:

  • mesh (Mesh) – A mesh with points and cells.

  • element (Element) – The finite element formulation to be applied on the cells.

  • quadrature (Quadrature) – An element-compatible numeric integration scheme with points and weights.

  • grad (bool, optional) – A flag to invoke gradient evaluation (default is True). If True, the partial derivatives of the element shape functions w.r.t. undeformed coordinates \(\frac{\partial \boldsymbol{h}(\boldsymbol{r})}{\partial \boldsymbol{X}}\) and the differential volumes \(dV\) are evaluated.

mesh#

A mesh with points and cells.

Type:

Mesh

element#

The finite element formulation to be applied on the cells.

Type:

Finite element

quadrature#

An element-compatible numeric integration scheme with points and weights.

Type:

Quadrature scheme

h#

Element shape function array h_aq of shape function a evaluated at quadrature point q.

Type:

ndarray

dhdr#

Partial derivative of element shape function array dhdr_aJq with shape function a w.r.t. natural element coordinate J evaluated at quadrature point q for every cell c (geometric gradient or Jacobian transformation between X and r).

Type:

ndarray

dXdr#

Geometric gradient dXdr_IJqc as partial derivative of undeformed coordinate I w.r.t. natural element coordinate J evaluated at quadrature point q for every cell c (geometric gradient or Jacobian transformation between X and r).

Type:

ndarray

drdX#

Inverse of dXdr.

Type:

ndarray

dV#

Numeric differential volume element as product of determinant of geometric gradient dV_qc = det(dXdr)_qc w_q and quadrature weight w_q, evaluated at quadrature point q for every cell c.

Type:

ndarray

dhdX#

Partial derivative of element shape functions dhdX_aJqc of shape function a w.r.t. undeformed coordinate J evaluated at quadrature point q for every cell c.

Type:

ndarray

Notes

The gradients of the element shape functions w.r.t the undeformed coordinates are evaluated at all integration points of each cell in the region if the optional gradient argument is True.

\[ \begin{align}\begin{aligned}\frac{\partial X_I}{\partial r_J} &= \hat{X}_{aI} \frac{ \partial h_a}{\partial r_J }\\\frac{\partial h_a}{\partial X_J} &= \frac{\partial h_a}{\partial r_I} \frac{\partial r_I}{\partial X_J}\\dV &= \det\left(\frac{\partial X_I}{\partial r_J}\right) w\end{aligned}\end{align} \]

Examples

>>> import felupe as fem

>>> mesh = fem.Rectangle(n=(3, 2))
>>> element = fem.Quad()
>>> quadrature = fem.GaussLegendre(order=1, dim=2)

>>> region = fem.Region(mesh, element, quadrature)
>>> region
<felupe Region object>
  Element formulation: Quad
  Quadrature rule: GaussLegendre
  Gradient evaluated: True

The numeric differential volumes are the products of the determinant of the geometric gradient \(\frac{\partial X_I}{\partial r_J}\) and the weights w of the quadrature points. The differential volume array is of shape (nquadraturepoints, ncells).

>>> region.dV
array([[0.125, 0.125],
       [0.125, 0.125],
       [0.125, 0.125],
       [0.125, 0.125]])

Cell-volumes may be obtained by cell-wise sums of the differential volumes located at the quadrature points.

>>> region.dV.sum(axis=0)
array([0.5, 0.5])

The partial derivative of the first element shape function w.r.t. the undeformed coordinates evaluated at the second integration point of the last element of the region:

>>> region.dhdX[0, :, 1, -1]
array([-1.57735027, -0.21132487])
copy(mesh=None, element=None, quadrature=None)[source]#

Return a copy of the region and reload it if necessary.

Parameters:

  • mesh (Mesh or None, optional) – A mesh with points and cells (default is None).

  • element (Element or None, optional) – The finite element formulation to be applied on the cells (default is None).

  • quadrature (Quadrature or None, optional) – An element-compatible numeric integration scheme with points and weights (default is None).

Returns:

A copy of the reloaded region.

Return type:

Region

See also

felupe.Region.reload

Reload the numeric region inplace.

plot(**kwargs)[source]#

Plot the element with point-ids and the quadrature points, scaled by their weights.

reload(mesh=None, element=None, quadrature=None)[source]#

Reload the numeric region inplace.

Parameters:

  • mesh (Mesh or None, optional) – A mesh with points and cells (default is None).

  • element (Element or None, optional) – The finite element formulation to be applied on the cells (default is None).

  • quadrature (Quadrature or None, optional) – An element-compatible numeric integration scheme with points and weights (default is None).

Examples

Warning

If the points of a mesh are modified and a region was already created with the mesh, it is important to re-evaluate (reload) the Region inplace.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=6)
>>> region = fem.RegionHexahedron(mesh)
>>> field = fem.FieldContainer([fem.Field(region, dim=3)])
>>>
>>> new_points = mesh.rotate(angle_deg=-90, axis=2).points
>>> mesh.update(points=new_points, callback=region.reload)

See also

felupe.Mesh.update

Update the mesh with given points and cells arrays inplace. Optionally, a callback is evaluated.

screenshot(filename=None, transparent_background=None, scale=None, **kwargs)[source]#

Take a screenshot of the element with the applied quadrature.

See also

pyvista.Plotter.screenshot

Take a screenshot of a PyVista plotter.

class felupe.RegionBoundary(mesh, element, quadrature, grad=True, only_surface=True, mask=None, ensure_3d=False)[source]#

A numeric boundary-region as a combination of a mesh, an element and a numeric integration scheme (quadrature rule).

Parameters:

  • mesh (Mesh) – A mesh with points and cells.

  • element (Element) – The finite element formulation to be applied on the cells.

  • quadrature (Quadrature) – An element-compatible numeric integration scheme with points and weights.

  • grad (bool, optional) – A flag to invoke gradient evaluation (default is True).

  • only_surface (bool, optional) – A flag to use only the enclosing outline of the region (default is True).

  • mask (ndarray or None, optional) – A boolean array to select a specific set of points (default is None).

  • ensure_3d (bool, optional) – A flag to enforce 3d area normal vectors.

mesh#

A mesh with points and cells.

Type:

Mesh

element#

The finite element formulation to be applied on the cells.

Type:

Finite element

quadrature#

An element-compatible numeric integration scheme with points and weights.

Type:

Quadrature scheme

h#

Element shape function array h_aq of shape function a evaluated at quadrature point q.

Type:

ndarray

dhdr#

Partial derivative of element shape function array dhdr_aJq with shape function a w.r.t. natural element coordinate J evaluated at quadrature point q for every cell c (geometric gradient or Jacobian transformation between X and r).

Type:

ndarray

dXdr#

Geometric gradient dXdr_IJqc as partial derivative of undeformed coordinate I w.r.t. natural element coordinate J evaluated at quadrature point q for every cell c (geometric gradient or Jacobian transformation between X and r).

Type:

ndarray

drdX#

Inverse of dXdr.

Type:

ndarray

dA#

Numeric Differential area vectors.

Type:

ndarray

normals#

Area unit normal vectors.

Type:

ndarray

dV#

Numeric Differential volume element as norm of Differential area vectors.

Type:

ndarray

dhdX#

Partial derivative of element shape functions dhdX_aJqc of shape function a w.r.t. undeformed coordinate J evaluated at quadrature point q for every cell c.

Type:

ndarray

Notes

The gradients of the element shape functions w.r.t the undeformed coordinates are evaluated at all integration points of each cell in the region if the optional gradient argument is True.

\[ \begin{align}\begin{aligned}\frac{\partial X_I}{\partial r_J} &= \hat{X}_{aI} \frac{ \partial h_a}{\partial r_J }\\\frac{\partial h_a}{\partial X_J} &= \frac{\partial h_a}{\partial r_I} \frac{\partial r_I}{\partial X_J}\\dV &= \det\left(\frac{\partial X_I}{\partial r_J}\right) w\end{aligned}\end{align} \]

Examples

>>> import felupe as fem

>>> mesh = fem.Rectangle(n=(3, 2))
>>> element = fem.Quad()
>>> quadrature = fem.GaussLegendreBoundary(order=1, dim=2)

>>> region = fem.RegionBoundary(mesh, element, quadrature)
>>> region
<felupe Region object>
  Element formulation: Quad
  Quadrature rule: GaussLegendreBoundary
  Gradient evaluated: True

The numeric differential area vectors are the products of the cofactors of the geometric gradient \(\partial X_I / \partial r_J\) and the weights w of the quadrature points. The differential area vectors array is of shape (nquadraturepoints, ndim, nboundarycells).

>>> region.dA
array([[[ 0.  , -0.5 ,  0.  ,  0.5 ,  0.  ,  0.  ],
        [ 0.  , -0.5 ,  0.  ,  0.5 ,  0.  ,  0.  ]],

       [[-0.25, -0.  , -0.25, -0.  ,  0.25,  0.25],
        [-0.25, -0.  , -0.25, -0.  ,  0.25,  0.25]]])

In a boundary region, the numeric differential volumes are the magnitudes of the differential area vectors. For a quad mesh, the boundary cell volumes are the edge lengths.

>>> region.dV.sum(axis=0)
array([0.5, 1. , 0.5, 1. , 0.5, 0.5])

Unit normal vectors are obtained by the ratio of the differential area vectors and the differential volumes.

>>> region.dA / region.dV  ## this is equal to ``region.normals``
array([[[ 0., -1.,  0.,  1.,  0.,  0.],
        [ 0., -1.,  0.,  1.,  0.,  0.]],

       [[-1., -0., -1., -0.,  1.,  1.],
        [-1., -0., -1., -0.,  1.,  1.]]])

The partial derivative of the first element shape function w.r.t. the undeformed coordinates evaluated at the second integration point of the last element of the region:

>>> region.dhdX[0, :, 1, -1]
array([2.        , 0.21132487])
copy(mesh=None, element=None, quadrature=None)#

Return a copy of the region and reload it if necessary.

Parameters:

  • mesh (Mesh or None, optional) – A mesh with points and cells (default is None).

  • element (Element or None, optional) – The finite element formulation to be applied on the cells (default is None).

  • quadrature (Quadrature or None, optional) – An element-compatible numeric integration scheme with points and weights (default is None).

Returns:

A copy of the reloaded region.

Return type:

Region

See also

felupe.Region.reload

Reload the numeric region inplace.

mesh_faces()[source]#

Return a Mesh with face-cells on the selected boundary.

plot(**kwargs)#

Plot the element with point-ids and the quadrature points, scaled by their weights.

reload(mesh=None, element=None, quadrature=None)#

Reload the numeric region inplace.

Parameters:

  • mesh (Mesh or None, optional) – A mesh with points and cells (default is None).

  • element (Element or None, optional) – The finite element formulation to be applied on the cells (default is None).

  • quadrature (Quadrature or None, optional) – An element-compatible numeric integration scheme with points and weights (default is None).

Examples

Warning

If the points of a mesh are modified and a region was already created with the mesh, it is important to re-evaluate (reload) the Region inplace.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube(n=6)
>>> region = fem.RegionHexahedron(mesh)
>>> field = fem.FieldContainer([fem.Field(region, dim=3)])
>>>
>>> new_points = mesh.rotate(angle_deg=-90, axis=2).points
>>> mesh.update(points=new_points, callback=region.reload)

See also

felupe.Mesh.update

Update the mesh with given points and cells arrays inplace. Optionally, a callback is evaluated.

screenshot(filename=None, transparent_background=None, scale=None, **kwargs)#

Take a screenshot of the element with the applied quadrature.

See also

pyvista.Plotter.screenshot

Take a screenshot of a PyVista plotter.

class felupe.RegionQuad(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendre object>, grad=True)[source]#

Bases: Region

A region with a quad element.

Examples

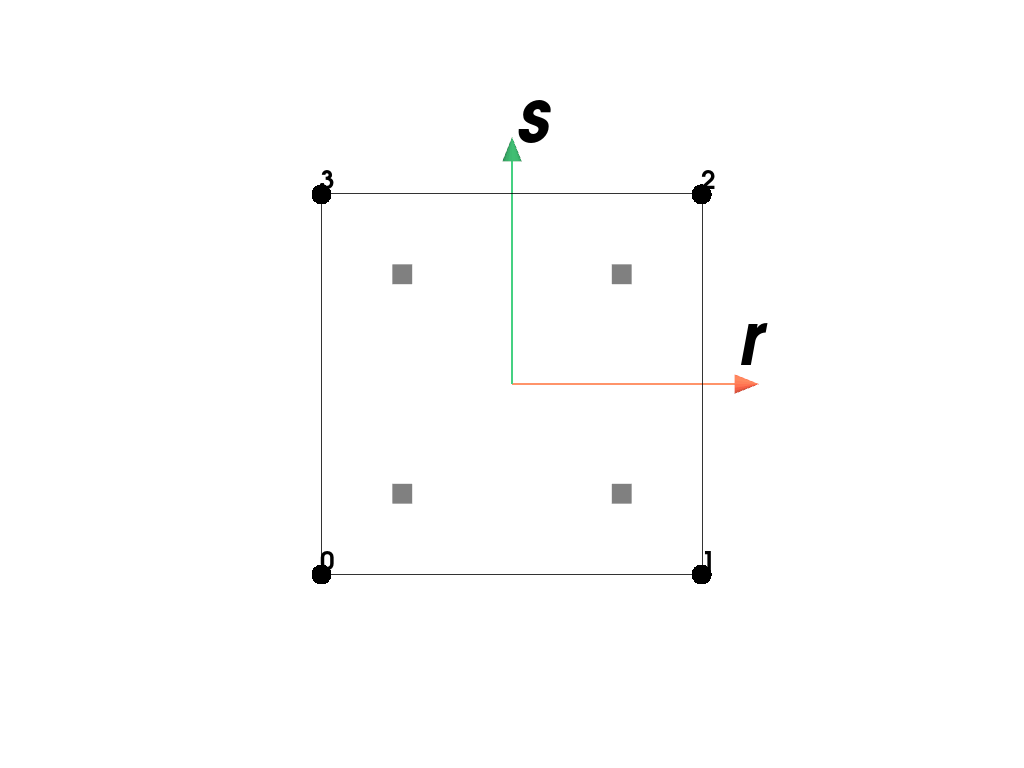
Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle()
>>> region = fem.RegionQuad(mesh)
>>> region
<felupe Region object>
  Element formulation: Quad
  Quadrature rule: GaussLegendre
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-1_00_00.png
class felupe.RegionQuadBoundary(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendreBoundary object>, grad=True, only_surface=True, mask=None, ensure_3d=False)[source]#

Bases: RegionBoundary

A region with a quad element.

Examples

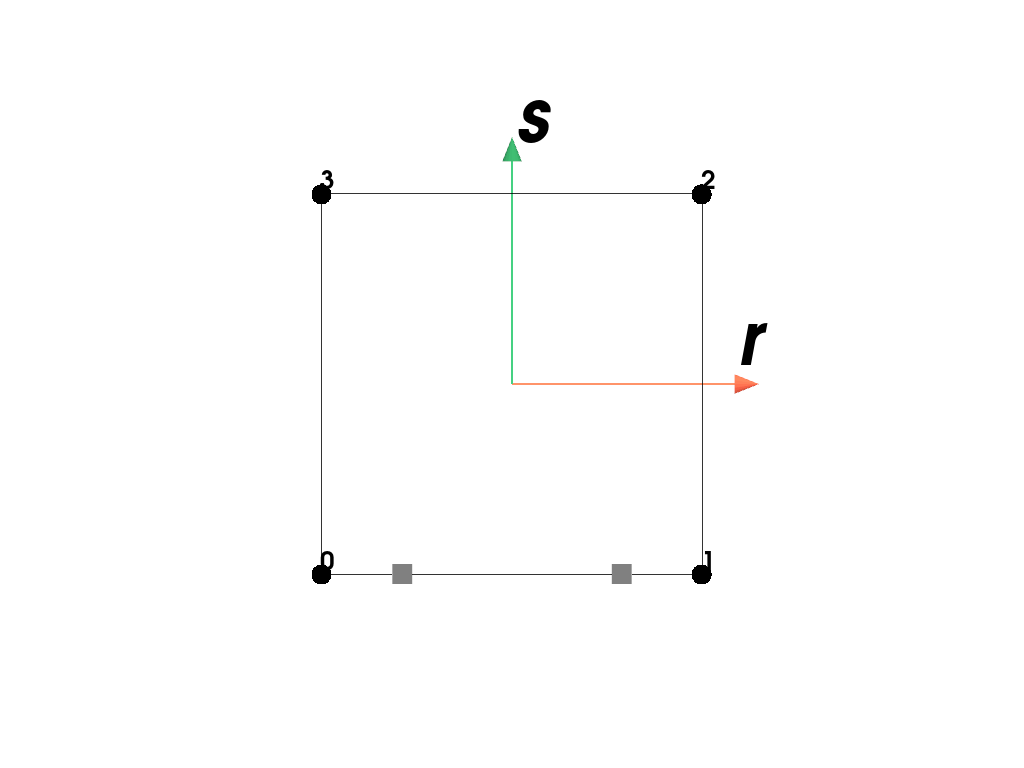
Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle()
>>> region = fem.RegionQuadBoundary(mesh)
>>> region
<felupe Region object>
  Element formulation: Quad
  Quadrature rule: GaussLegendreBoundary
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-2_00_00.png
class felupe.RegionHexahedronBoundary(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendreBoundary object>, grad=True, only_surface=True, mask=None)[source]#

Bases: RegionBoundary

A boundary region with a hexahedron element.

Examples

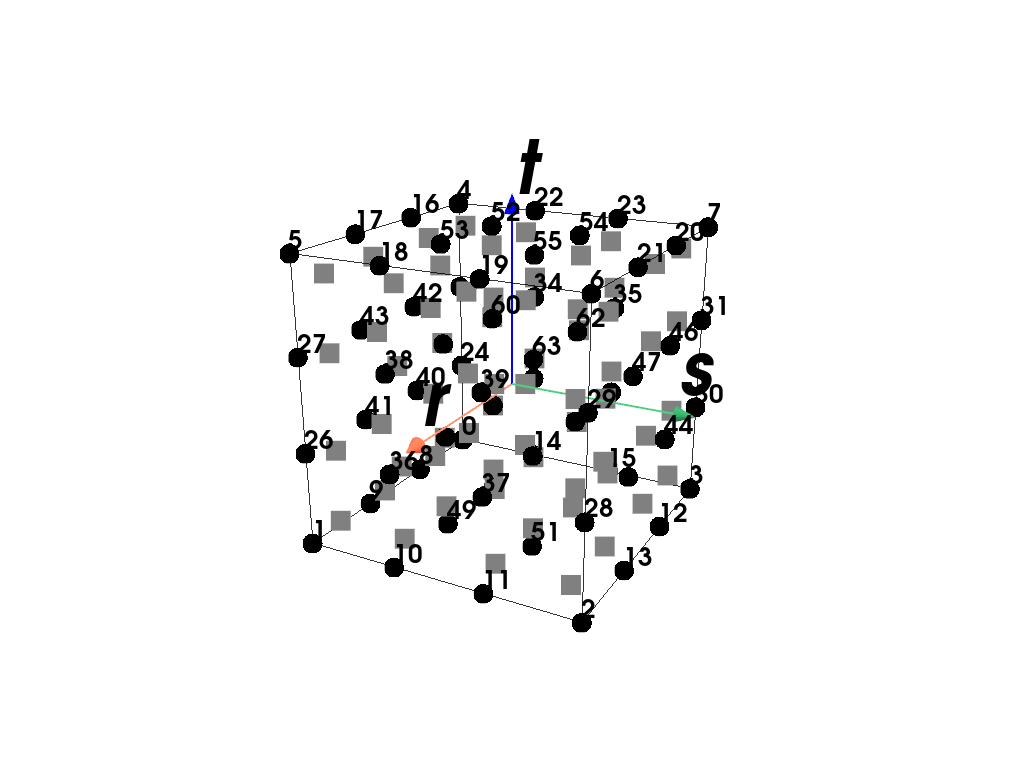
Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube()
>>> region = fem.RegionHexahedronBoundary(mesh)
>>> region
<felupe Region object>
  Element formulation: Hexahedron
  Quadrature rule: GaussLegendreBoundary
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-3_00_00.png
class felupe.RegionHexahedron(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendre object>, grad=True)[source]#

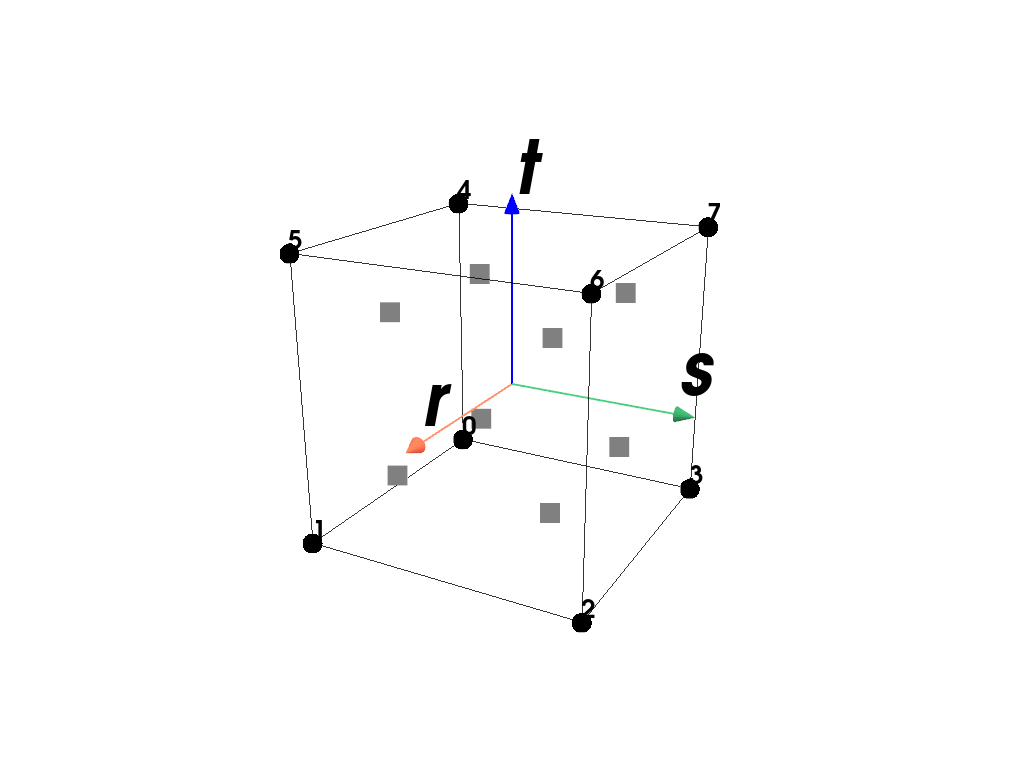
Bases: Region

A region with a hexahedron element.

Examples

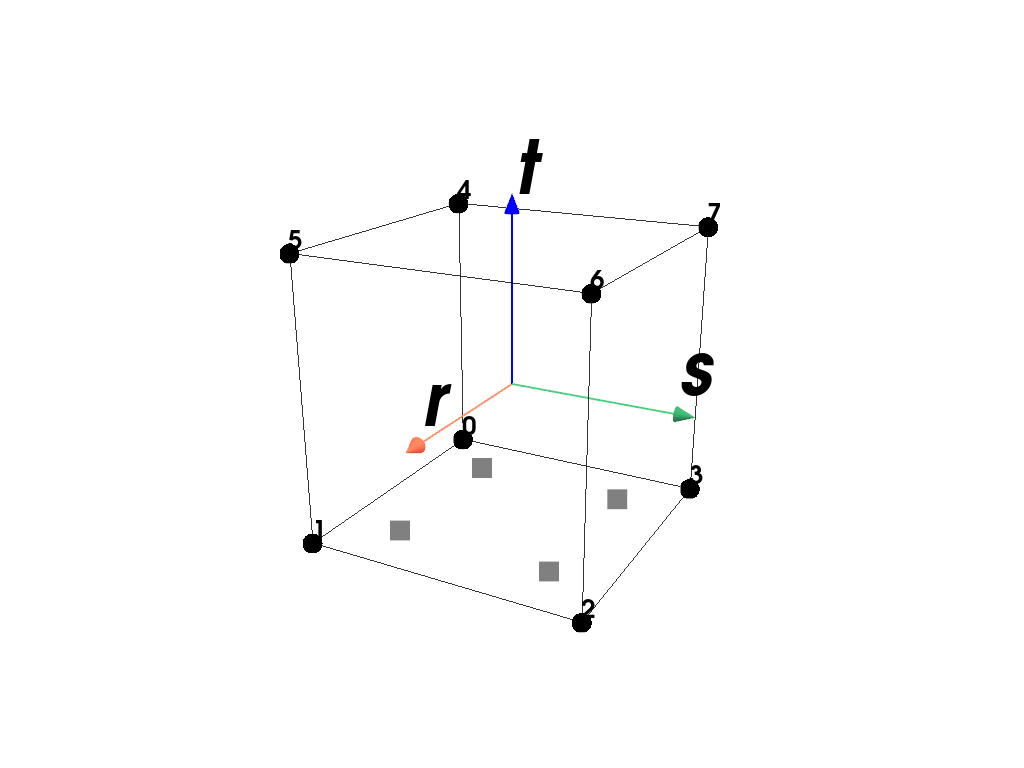
Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube()
>>> region = fem.RegionHexahedron(mesh)
>>> region
<felupe Region object>
  Element formulation: Hexahedron
  Quadrature rule: GaussLegendre
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-4_00_00.png
class felupe.RegionTriangle(mesh, quadrature=<felupe.quadrature._triangle.Triangle object>, grad=True)[source]#

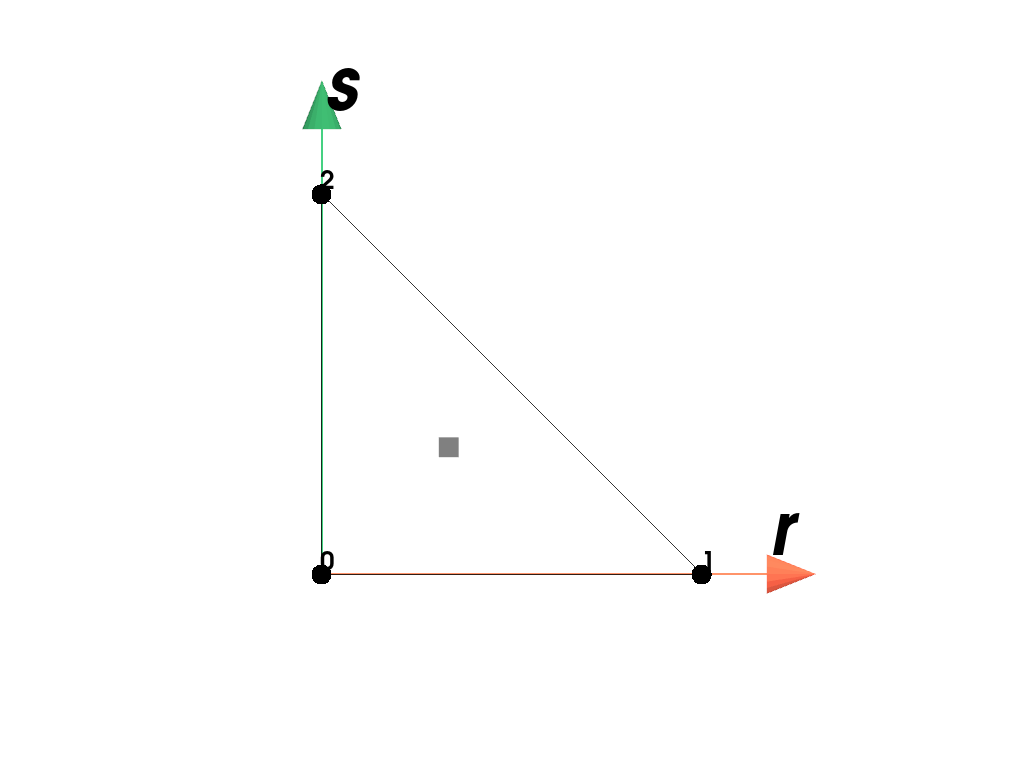
Bases: Region

A region with a triangle element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.mesh.Rectangle().triangulate()
>>> region = fem.RegionTriangle(mesh)
>>> region
<felupe Region object>
  Element formulation: Triangle
  Quadrature rule: Triangle
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-5_00_00.png
class felupe.RegionTetra(mesh, quadrature=<felupe.quadrature._tetra.Tetrahedron object>, grad=True)[source]#

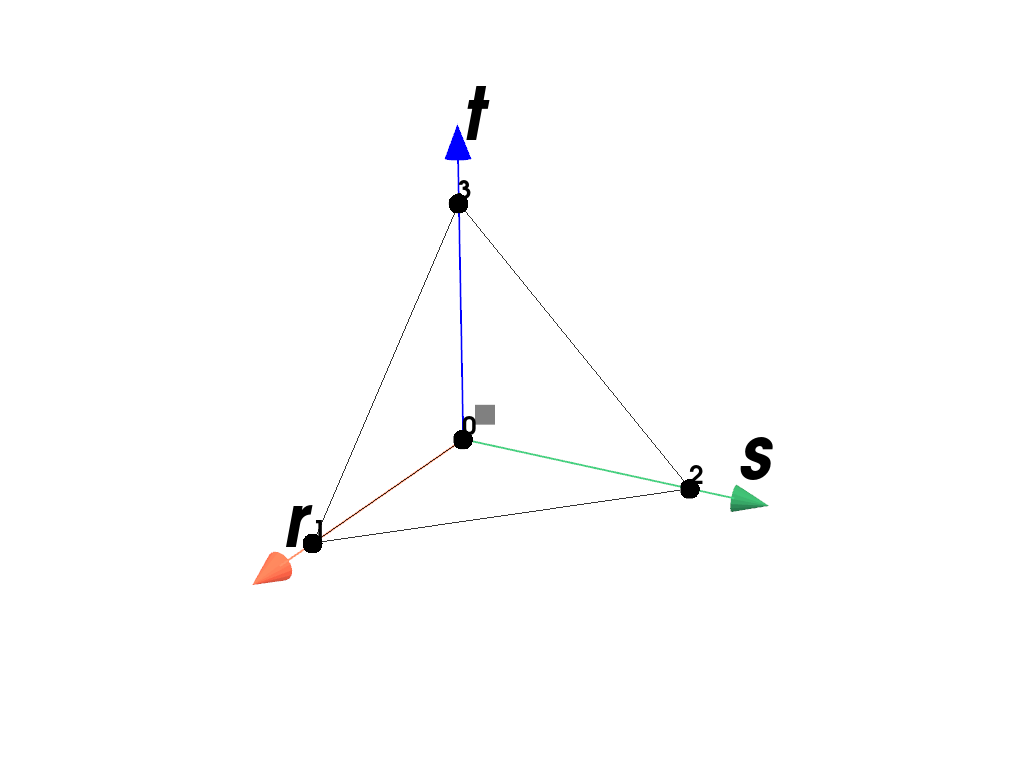
Bases: Region

A region with a tetra element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube().triangulate()
>>> region = fem.RegionTetra(mesh)
>>> region
<felupe Region object>
  Element formulation: Tetra
  Quadrature rule: Tetrahedron
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-6_00_00.png
class felupe.RegionConstantQuad(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendre object>, grad=False)[source]#

Bases: Region

A region with a constant quad element.

class felupe.RegionQuadraticQuad(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendre object>, grad=True)[source]#

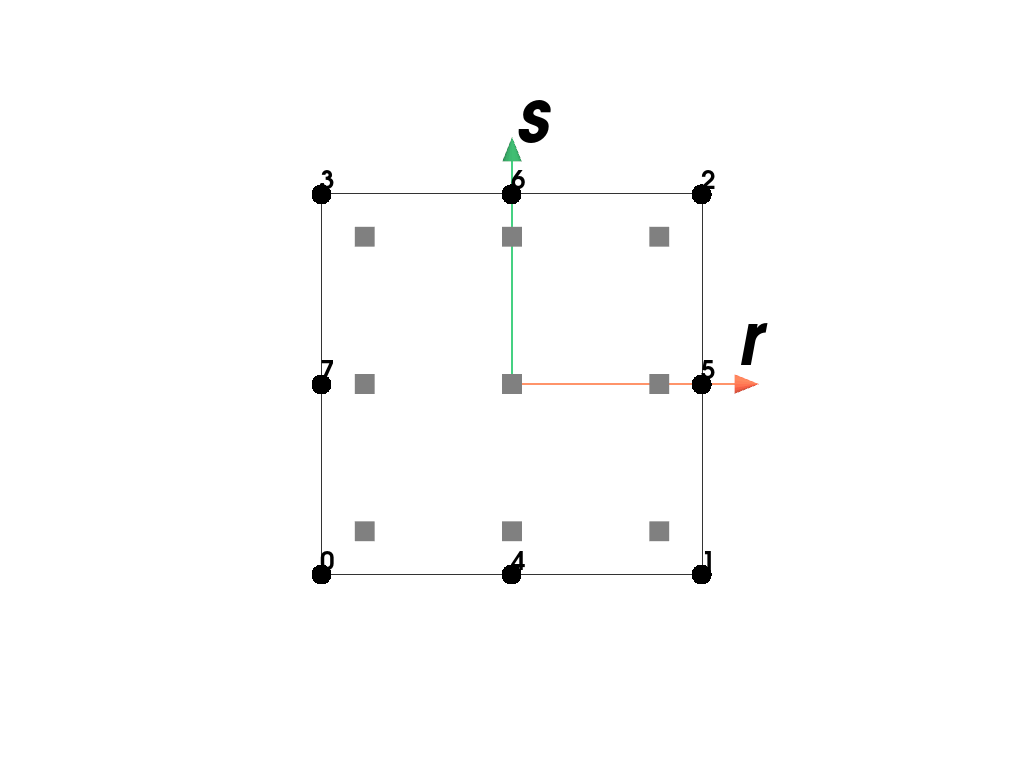
Bases: Region

A region with a (serendipity) quadratic quad element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle().add_midpoints_edges()
>>> region = fem.RegionQuadraticQuad(mesh)
>>> region
<felupe Region object>
  Element formulation: QuadraticQuad
  Quadrature rule: GaussLegendre
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-7_00_00.png
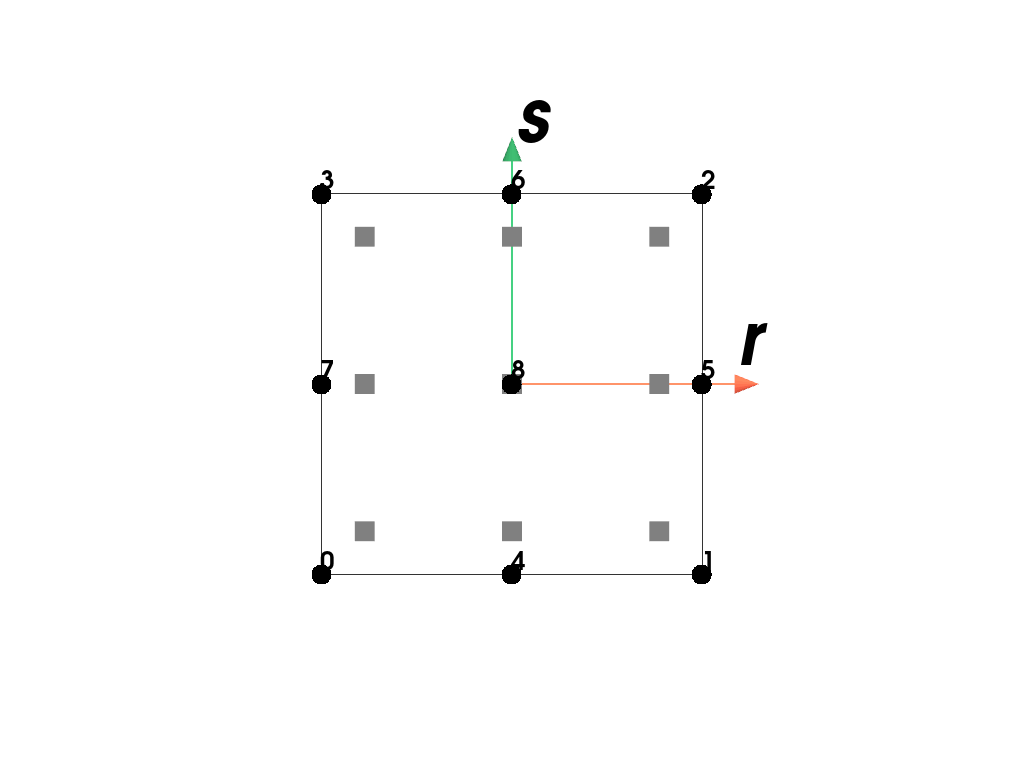
class felupe.RegionBiQuadraticQuad(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendre object>, grad=True)[source]#

Bases: Region

A region with a bi-quadratic (Lagrange) quad element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> rect = fem.Rectangle()
>>> mesh = rect.add_midpoints_edges().add_midpoints_faces()
>>> region = fem.RegionBiQuadraticQuad(mesh)
>>> region
<felupe Region object>
  Element formulation: BiQuadraticQuad
  Quadrature rule: GaussLegendre
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-8_00_00.png
class felupe.RegionConstantHexahedron(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendre object>, grad=False)[source]#

Bases: Region

A region with a constant hexahedron element.

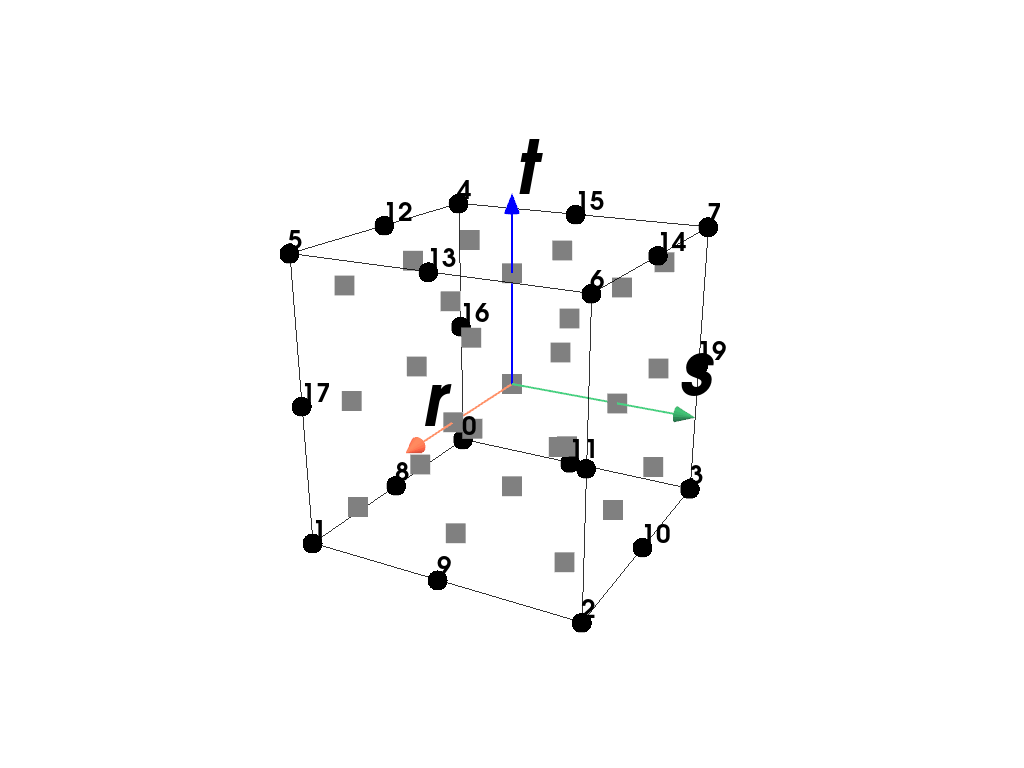
class felupe.RegionQuadraticHexahedron(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendre object>, grad=True)[source]#

Bases: Region

A region with a (serendipity) quadratic hexahedron element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube().add_midpoints_edges()
>>> region = fem.RegionQuadraticHexahedron(mesh)
>>> region
<felupe Region object>
  Element formulation: QuadraticHexahedron
  Quadrature rule: GaussLegendre
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-9_00_00.png
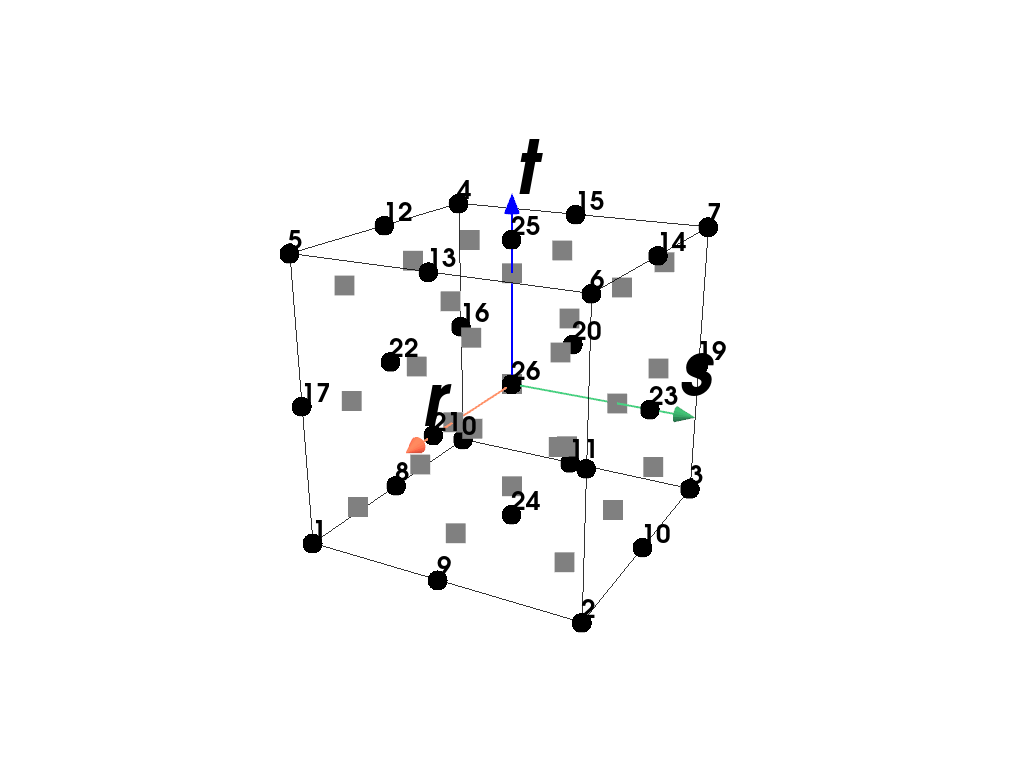
class felupe.RegionTriQuadraticHexahedron(mesh, quadrature=<felupe.quadrature._gausslegendre.GaussLegendre object>, grad=True)[source]#

Bases: Region

A region with a tri-quadratic (Lagrange) hexahedron element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> cube = fem.Cube().add_midpoints_edges()
>>> mesh = cube.add_midpoints_faces().add_midpoints_volumes()
>>> region = fem.RegionTriQuadraticHexahedron(mesh)
>>> region
<felupe Region object>
  Element formulation: TriQuadraticHexahedron
  Quadrature rule: GaussLegendre
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-10_00_00.png
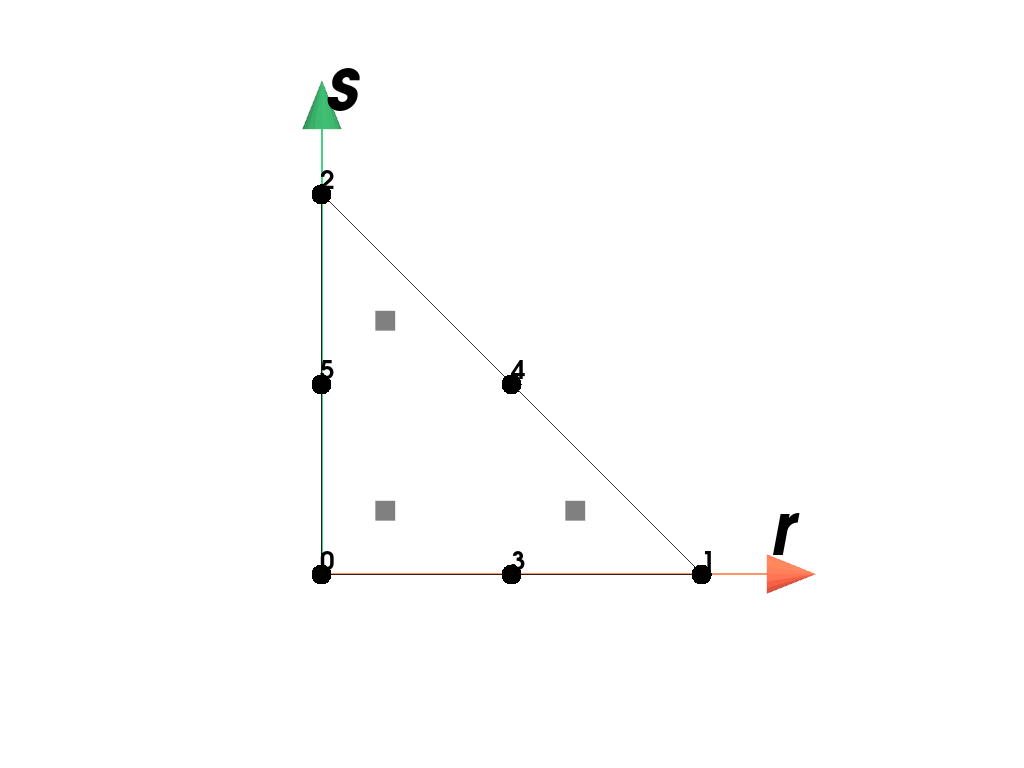
class felupe.RegionQuadraticTriangle(mesh, quadrature=<felupe.quadrature._triangle.Triangle object>, grad=True)[source]#

Bases: Region

A region with a quadratic triangle element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle().triangulate().add_midpoints_edges()
>>> region = fem.RegionQuadraticTriangle(mesh)
>>> region
<felupe Region object>
  Element formulation: QuadraticTriangle
  Quadrature rule: Triangle
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-11_00_00.png
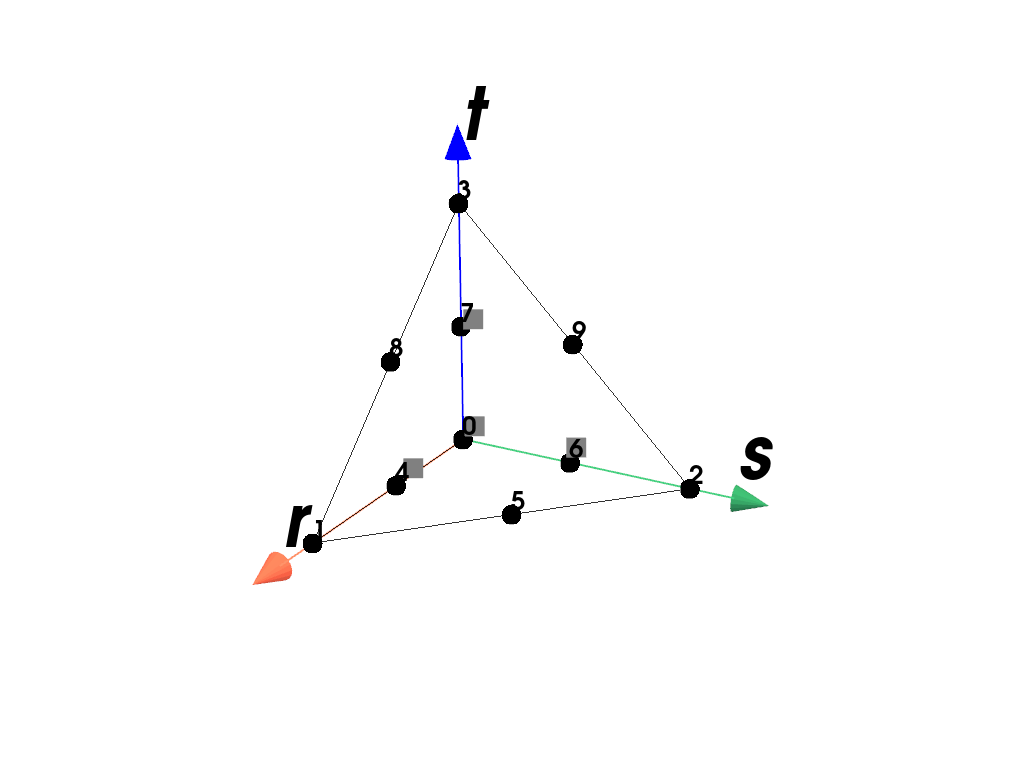
class felupe.RegionQuadraticTetra(mesh, quadrature=<felupe.quadrature._tetra.Tetrahedron object>, grad=True)[source]#

Bases: Region

A region with a quadratic tetra element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube().triangulate().add_midpoints_edges()
>>> region = fem.RegionQuadraticTetra(mesh)
>>> region
<felupe Region object>
  Element formulation: QuadraticTetra
  Quadrature rule: Tetrahedron
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-12_00_00.png
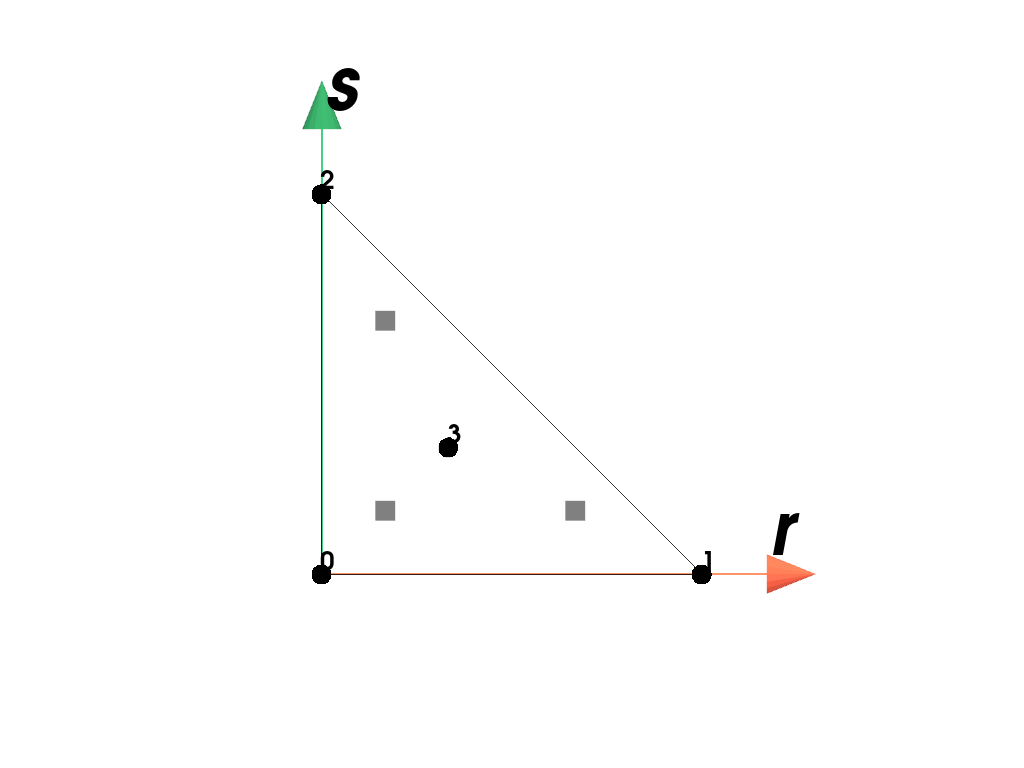
class felupe.RegionTriangleMINI(mesh, quadrature=<felupe.quadrature._triangle.Triangle object>, grad=True, bubble_multiplier=0.1)[source]#

Bases: Region

A region with a triangle-MINI element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Rectangle().triangulate().add_midpoints_faces()
>>> region = fem.RegionTriangleMINI(mesh)
>>> region
<felupe Region object>
  Element formulation: TriangleMINI
  Quadrature rule: Triangle
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-13_00_00.png
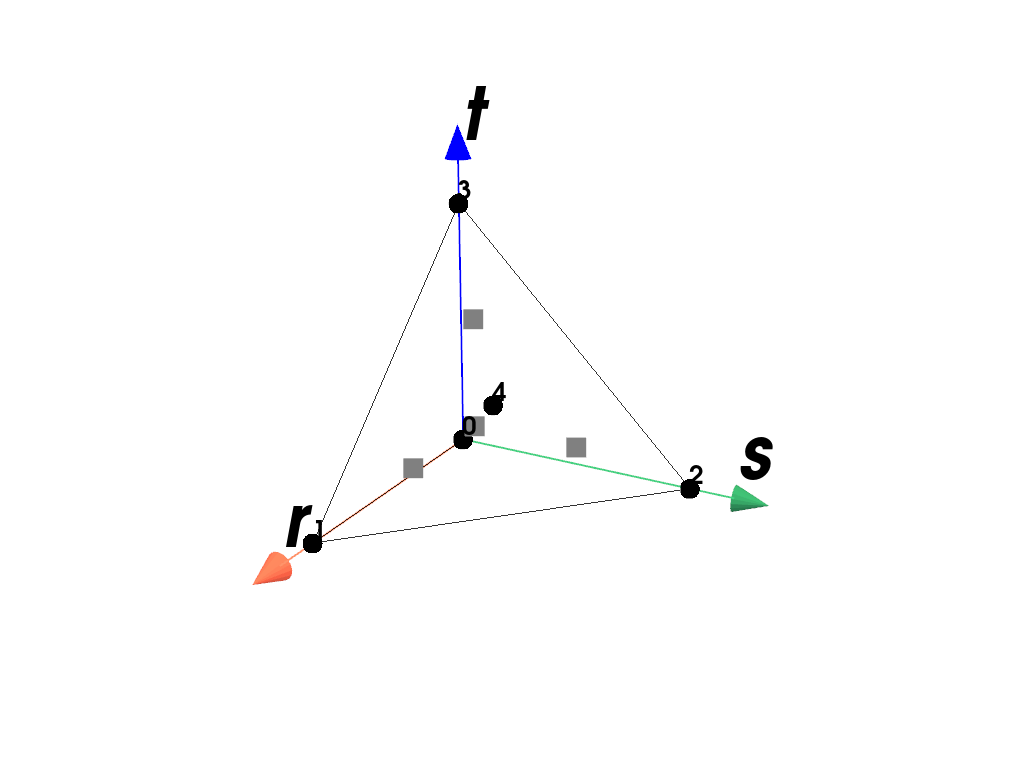
class felupe.RegionTetraMINI(mesh, quadrature=<felupe.quadrature._tetra.Tetrahedron object>, grad=True, bubble_multiplier=0.1)[source]#

Bases: Region

A region with a tetra-MINI element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.Cube().triangulate().add_midpoints_volumes()
>>> region = fem.RegionTetraMINI(mesh)
>>> region
<felupe Region object>
  Element formulation: TetraMINI
  Quadrature rule: Tetrahedron
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-14_00_00.png
class felupe.RegionLagrange(mesh, order, dim, quadrature=None, grad=True, permute=True)[source]#

Bases: Region

A region with an arbitrary order Lagrange element.

Examples

Plot the element with its point-ids and the applied quadrature rule.

>>> import felupe as fem
>>>
>>> mesh = fem.mesh.CubeArbitraryOrderHexahedron(order=3)
>>> region = fem.RegionLagrange(mesh, order=3, dim=3)
>>> region
<felupe Region object>
  Element formulation: ArbitraryOrderLagrange
  Quadrature rule: GaussLegendre
  Gradient evaluated: True

>>> region.plot().show()
../_images/region-15_00_00.png
On this page
Show Source