Quadrature

This module contains quadrature (numeric integration) schemes for different finite element formulations. The integration points of a boundary-quadrature are located on the first edge for 2d elements and on the first face for 3d elements.

Lines, Quads and Hexahedrons

GaussLegendre(order, dim[, permute])	An arbitrary-order Gauss-Legendre quadrature rule of dimension 1, 2 or 3 on the interval \([-1, 1]\).
GaussLegendreBoundary(order, dim[, permute])	An arbitrary-order Gauss-Legendre quadrature rule of dim 1, 2 or 3 on the interval [-1, 1].

Triangles and Tetrahedrons

quadrature.Triangle(order)	A quadrature scheme suitable for Triangles of order 1, 2 or 3 on the interval \([0, 1]\).
quadrature.Tetrahedron(order)	A quadrature scheme suitable for Tetrahedrons of order 1, 2 or 3 on the interval \([0, 1]\).
TriangleQuadrature	alias of Triangle
TetrahedronQuadrature	alias of Tetrahedron

Sphere

BazantOh([n])

Quadrature scheme for a numeric integration of the surface of a unit sphere [1]_.

Detailed API Reference

class felupe.quadrature.Scheme(points, weights)

Bases: object

A quadrature scheme with integration points \(x_q\) and weights \(w_q\). It approximates the integral of a function over a region \(V\) by a weighted sum of function values \(f_q = f(x_q)\), evaluated on the quadrature-points.

Notes

The approximation is given by

\[\int_V f(x) dV \approx \sum f(x_q) w_q\]

with quadrature points \(x_q\) and corresponding weights \(w_q\).

plot(plotter=None, point_size=20, weighted=False, **kwargs)

Plot the quadrature points, scaled by their weights, into a (optionally provided) PyVista plotter.

See also

felupe.Scene.plot

Plot method of a scene.

screenshot(*args, filename=None, transparent_background=None, scale=None, **kwargs)

Take a screenshot of the quadrature.

See also

pyvista.Plotter.screenshot

Take a screenshot of a PyVista plotter.

class felupe.GaussLegendre(order: int, dim: int, permute: bool = True)

Bases: Scheme

An arbitrary-order Gauss-Legendre quadrature rule of dimension 1, 2 or 3 on the interval \([-1, 1]\).

Parameters:

• order (int) – The number of sample points \(n\) minus one. The quadrature rule integrates degree \(2n-1\) polynomials exactly.

• dim (int) – The dimension of the quadrature region.

• permute (bool, optional) – Permute the quadrature points according to the cell point orderings (default is True). This is supported for two and three dimensions as well as first and second order schemes. Otherwise this flag is silently ignored.

Notes

The approximation is given by

\[\int_{-1}^1 f(x) dx \approx \sum f(x_q) w_q\]

with quadrature points \(x_q\) and corresponding weights \(w_q\).

Examples

>>> import felupe as fem
>>>
>>> element = fem.Line()
>>> quadrature = fem.GaussLegendre(order=2, dim=1)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

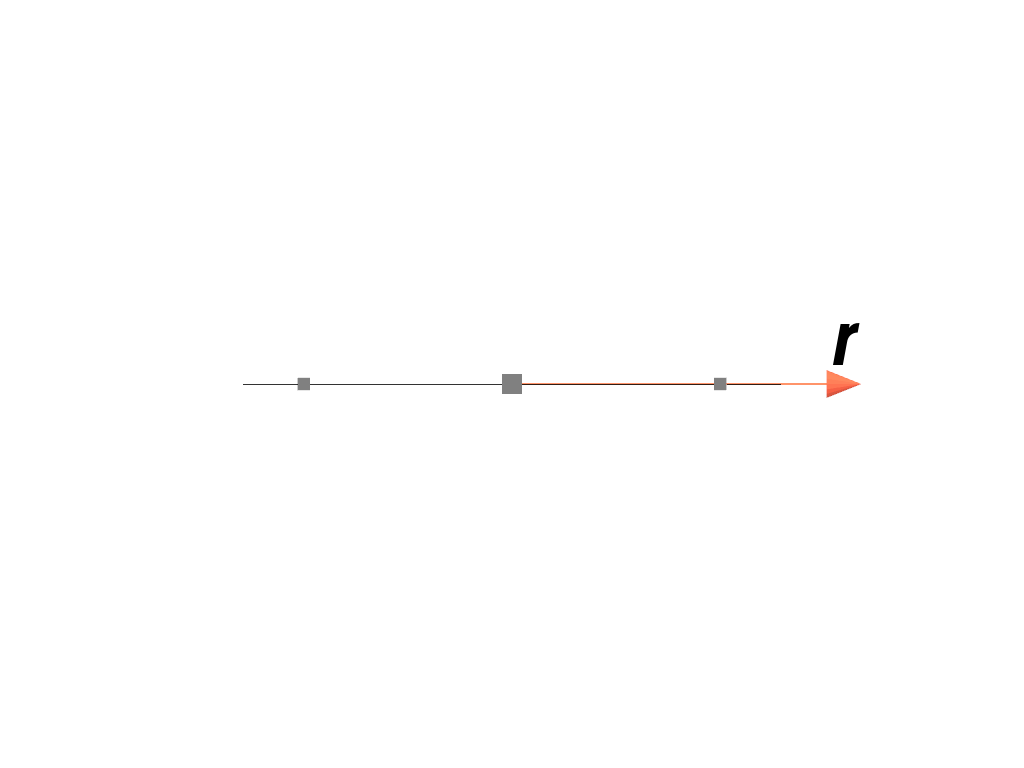
>>> import felupe as fem
>>>
>>> element = fem.QuadraticQuad()
>>> quadrature = fem.GaussLegendre(order=2, dim=2)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

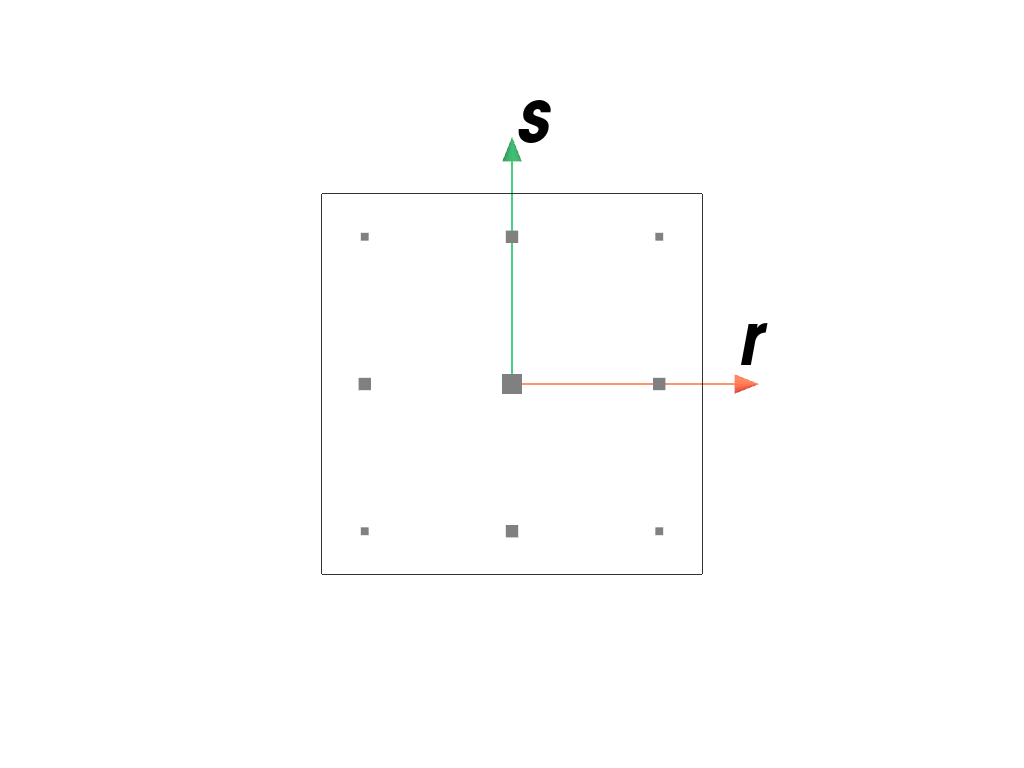
>>> import felupe as fem
>>>
>>> element = fem.QuadraticHexahedron()
>>> quadrature = fem.GaussLegendre(order=2, dim=3)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

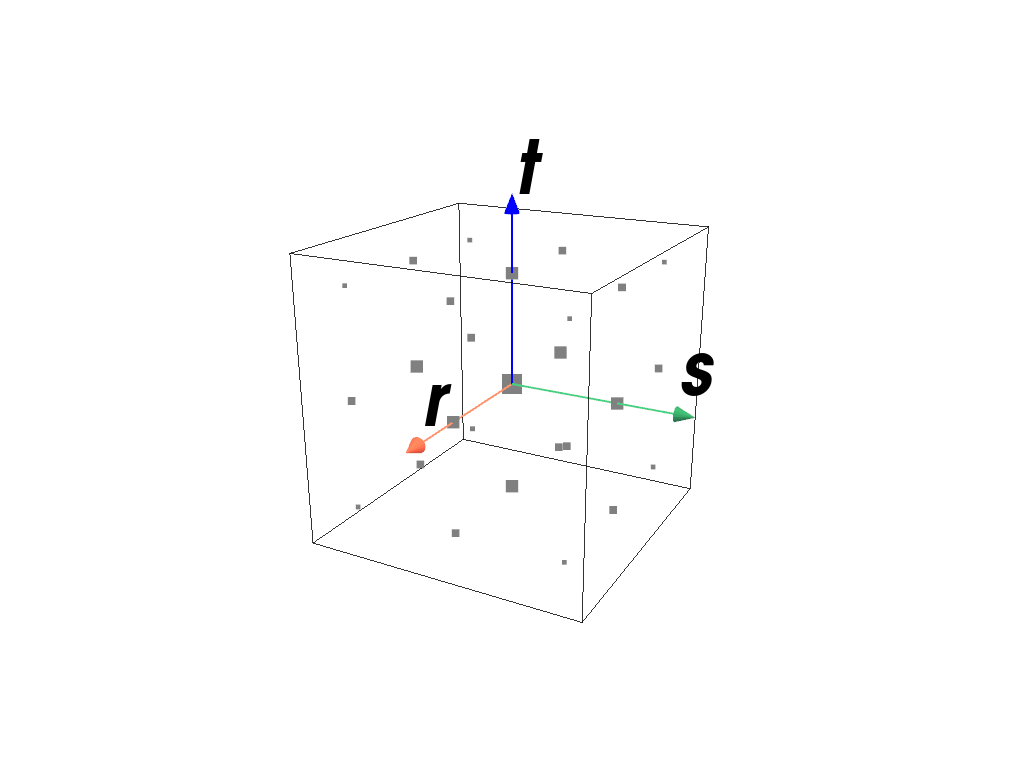
>>> import felupe as fem
>>>
>>> element = fem.ArbitraryOrderLagrangeElement(order=5, dim=2)
>>> quadrature = fem.GaussLegendre(order=5, dim=2)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

inv()

Return the inverse quadrature scheme.

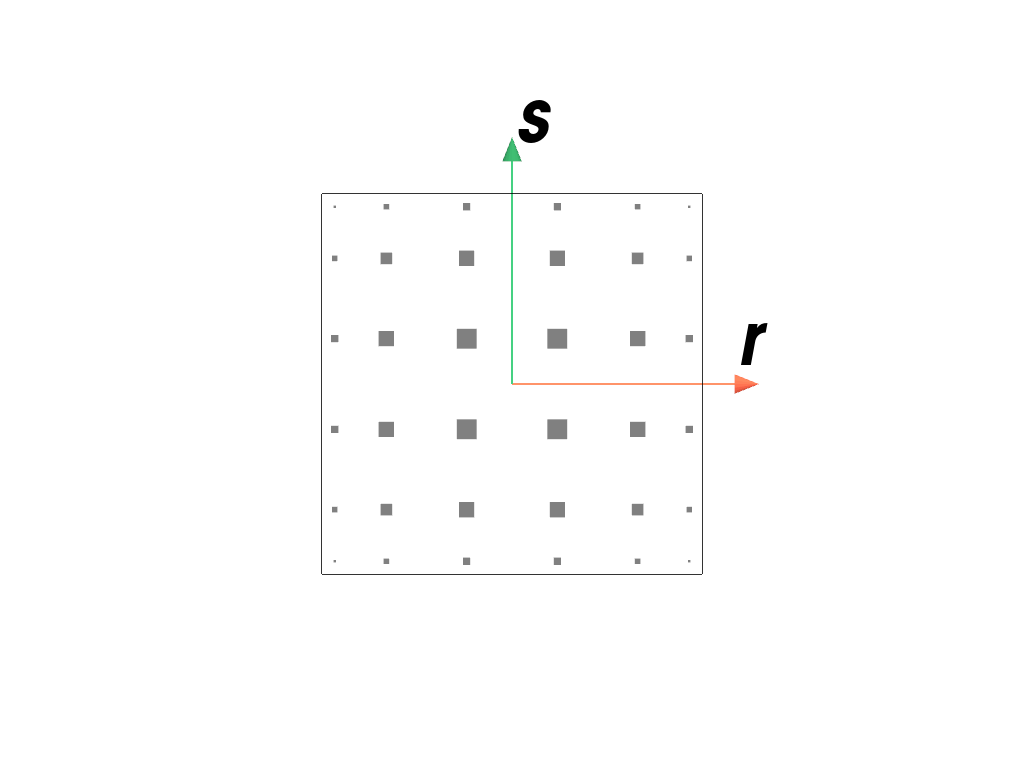
class felupe.GaussLegendreBoundary(order: int, dim: int, permute: bool = True)

Bases: GaussLegendre

An arbitrary-order Gauss-Legendre quadrature rule of dim 1, 2 or 3 on the interval [-1, 1].

Parameters:

• order (int) – The number of sample points \(n\) minus one. The quadrature rule integrates degree \(2n-1\) polynomials exactly.

• dim (int) – The dimension of the quadrature region.

• permute (bool, optional) – Permute the quadrature points according to the cell point orderings (default is True).

Notes

The approximation is given by

\[\int_{-1}^1 f(x) dx \approx \sum f(x_q) w_q\]

with quadrature points \(x_q\) and corresponding weights \(w_q\).

Examples

>>> import felupe as fem
>>>
>>> element = fem.QuadraticQuad()
>>> quadrature = fem.GaussLegendreBoundary(order=2, dim=2)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

Static Scene

Interactive Scene

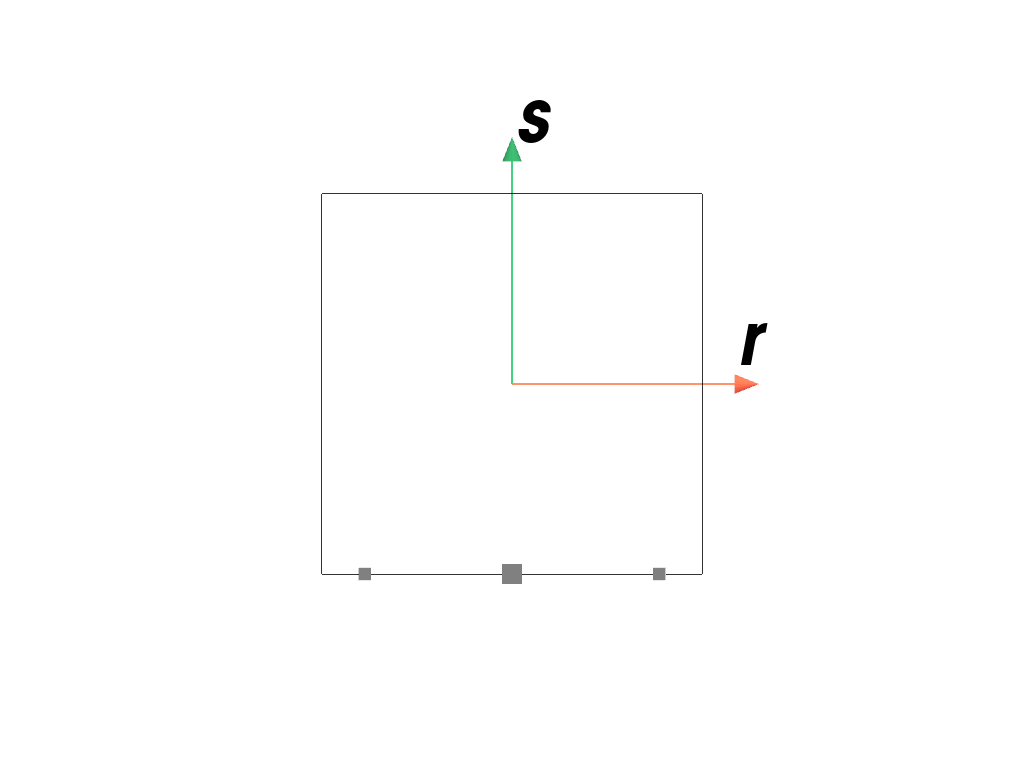
>>> import felupe as fem
>>>
>>> element = fem.QuadraticHexahedron()
>>> quadrature = fem.GaussLegendreBoundary(order=2, dim=3)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

Static Scene

Interactive Scene

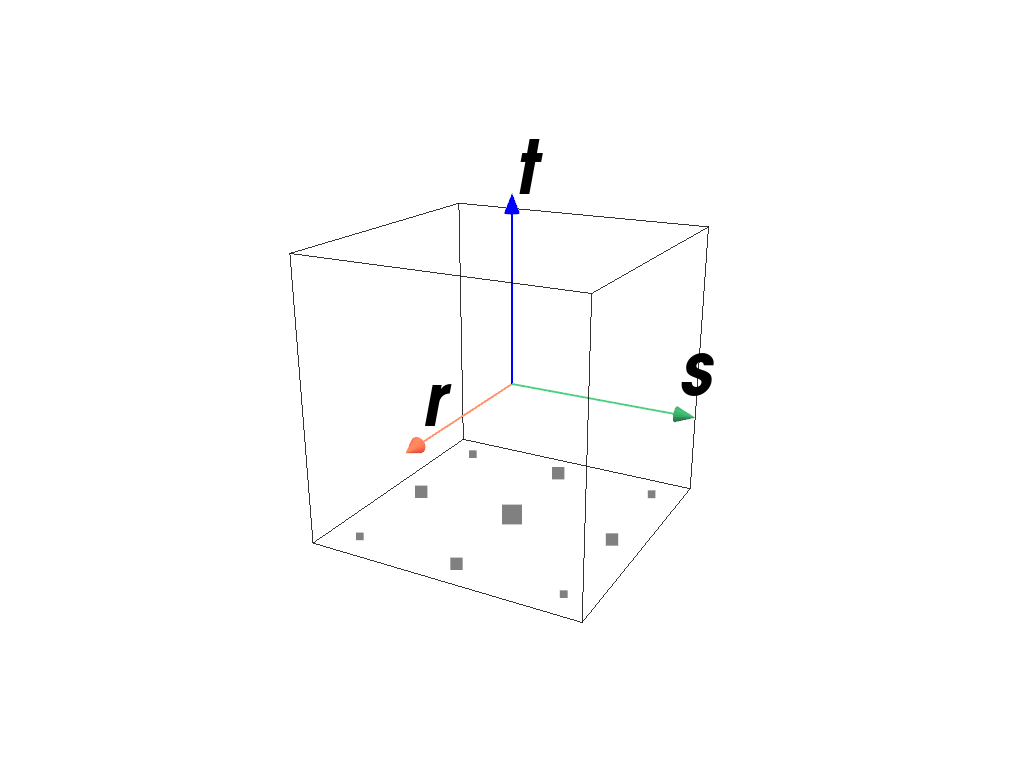
>>> import felupe as fem
>>>
>>> element = fem.ArbitraryOrderLagrangeElement(order=5, dim=3)
>>> quadrature = fem.GaussLegendreBoundary(order=5, dim=3)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

Static Scene

Interactive Scene

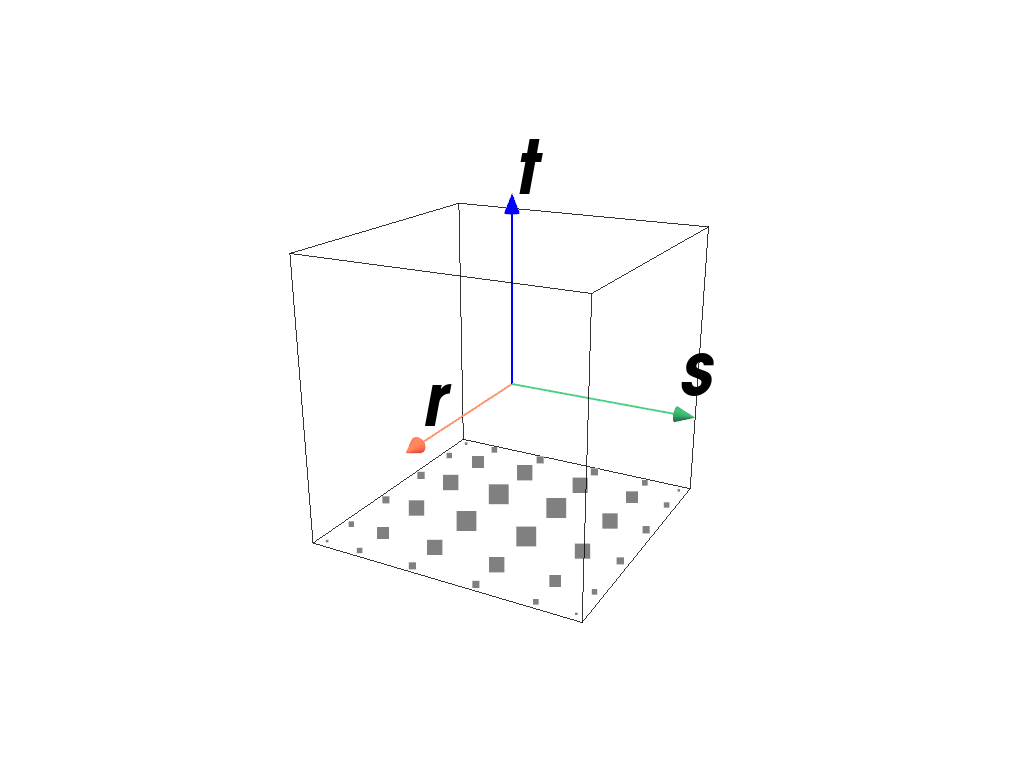
class felupe.quadrature.Triangle(order: int)

Bases: Scheme

A quadrature scheme suitable for Triangles of order 1, 2 or 3 on the interval \([0, 1]\).

Parameters:

order (int) – The order of the quadrature scheme.

Notes

The approximation is given by

\[\int_A f(x) dA \approx \sum f(x_q) w_q\]

with quadrature points \(x_q\) and corresponding weights \(w_q\) [1]_ [2].

Examples

>>> import felupe as fem
>>>
>>> element = fem.Triangle()
>>> quadrature = fem.TriangleQuadrature(order=1)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

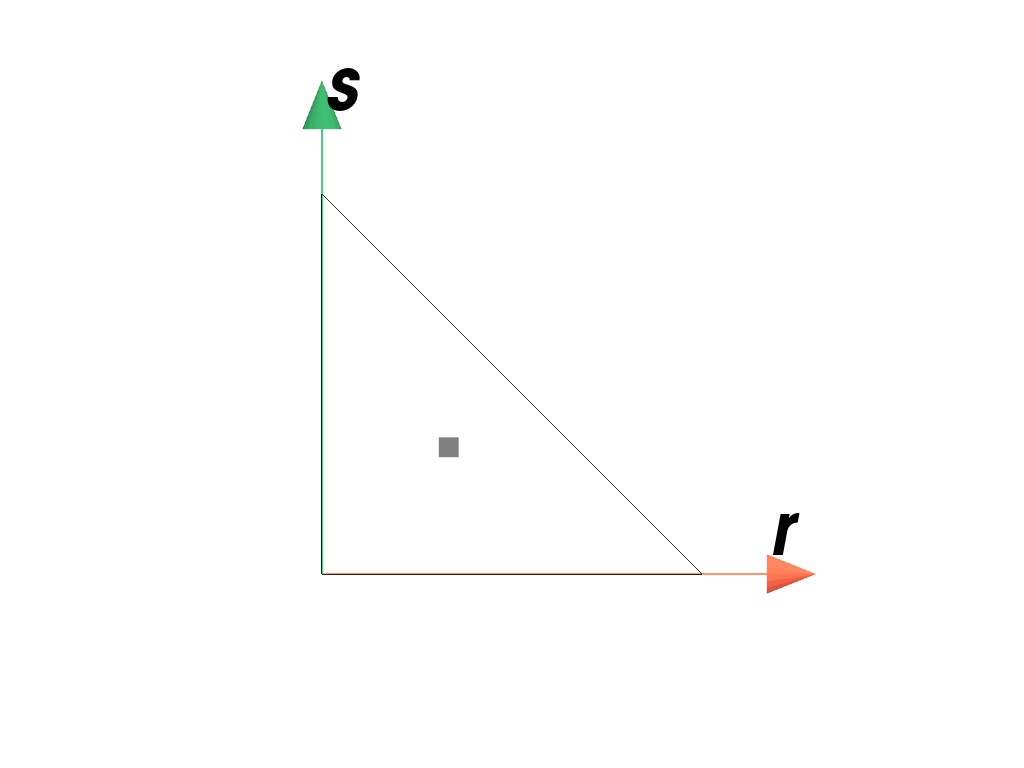
>>> import felupe as fem
>>>
>>> element = fem.QuadraticTriangle()
>>> quadrature = fem.TriangleQuadrature(order=2)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

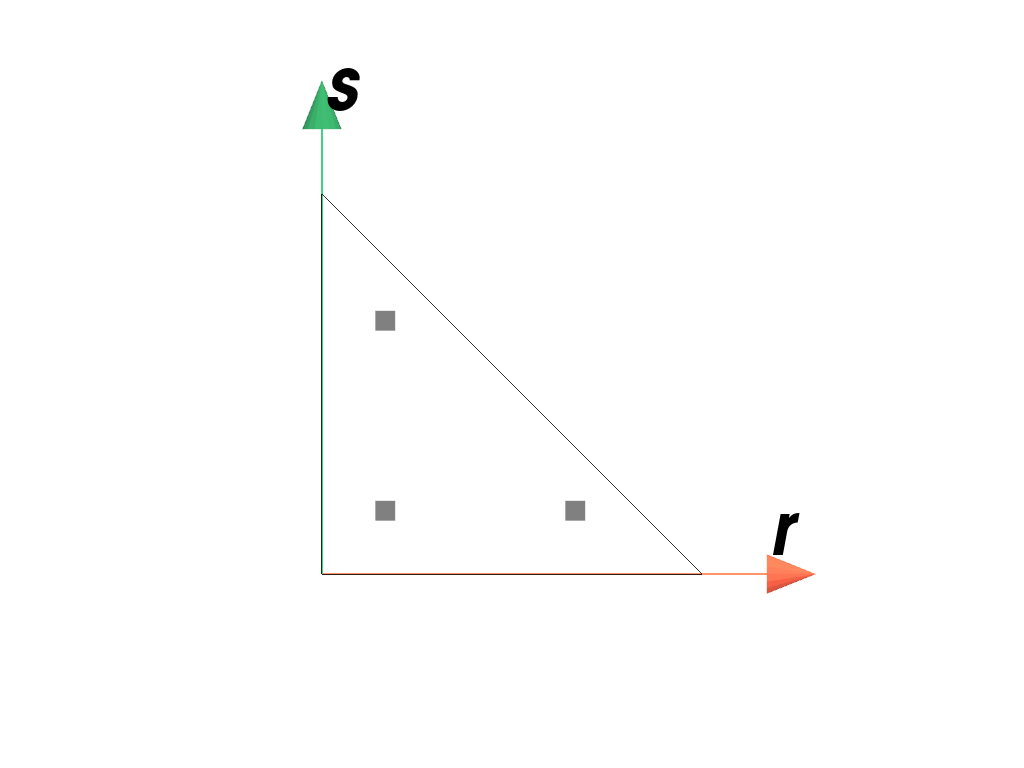
>>> import felupe as fem
>>>
>>> element = fem.QuadraticTriangle()
>>> quadrature = fem.TriangleQuadrature(order=5)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

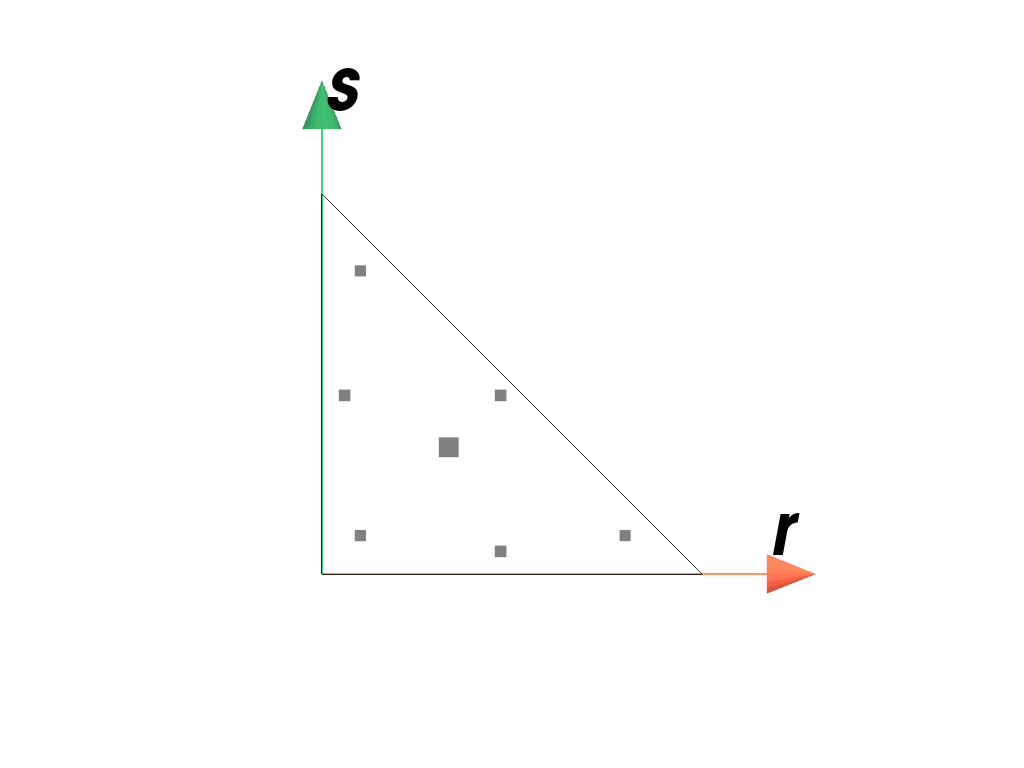
References

[1]

K. J. Bathe, Finite element procedures, 2nd ed. K. J. Bathe, Watertown, MA, 2014.

[2]

O. C. Zienkiewicz, R. L. Taylor and J. Z. Zhu, The Finite Element Method: Its Basis and Fundamentals, 7th ed., Elsevier, 2013.

class felupe.quadrature.Tetrahedron(order: int)

Bases: Scheme

A quadrature scheme suitable for Tetrahedrons of order 1, 2 or 3 on the interval \([0, 1]\).

Parameters:

order (int) – The order of the quadrature scheme.

Notes

The approximation is given by

\[\int_V f(x) dV \approx \sum f(x_q) w_q\]

with quadrature points \(x_q\) and corresponding weights \(w_q\) [1]_.

Examples

>>> import felupe as fem
>>>
>>> element = fem.Tetra()
>>> quadrature = fem.TetrahedronQuadrature(order=1)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

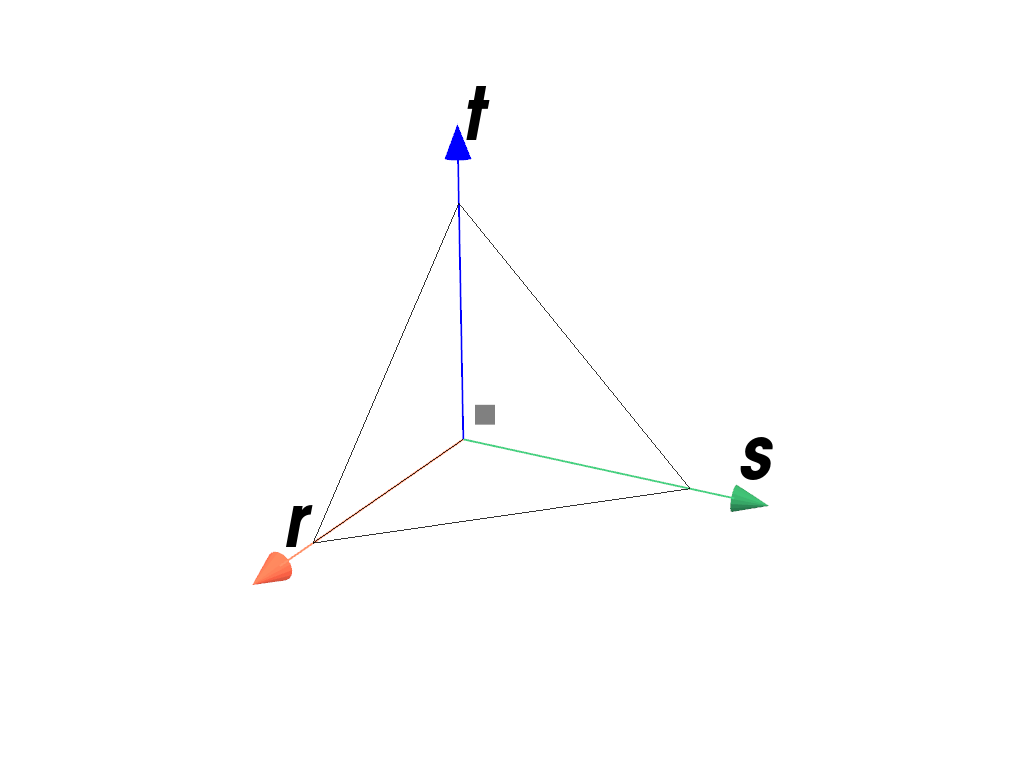
>>> import felupe as fem
>>>
>>> element = fem.QuadraticTetra()
>>> quadrature = fem.TetrahedronQuadrature(order=2)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

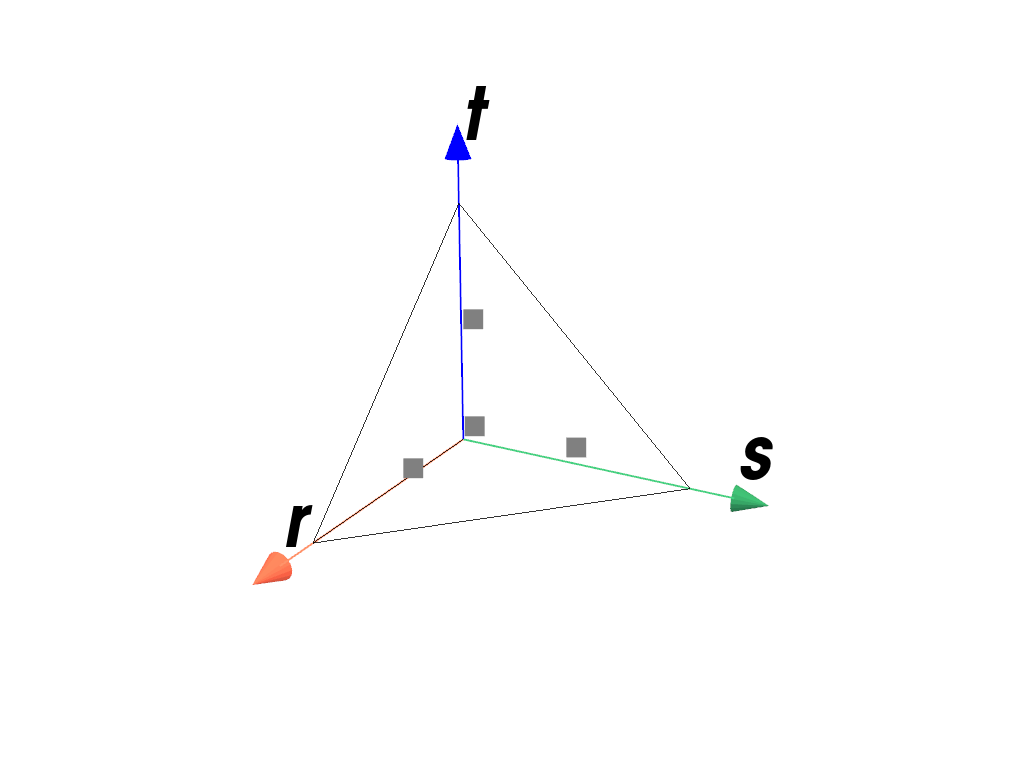
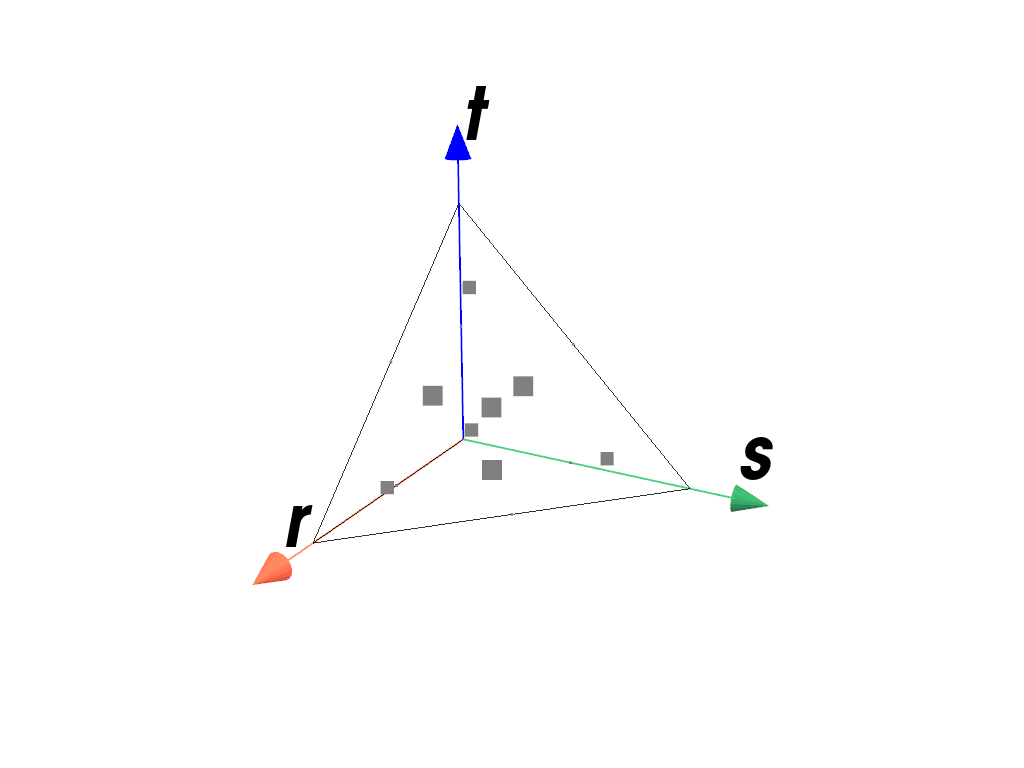
>>> import felupe as fem
>>>
>>> element = fem.QuadraticTetra()
>>> quadrature = fem.TetrahedronQuadrature(order=5)
>>> quadrature.plot(
...     plotter=element.plot(add_point_labels=False, show_points=False),
...     weighted=True,
... ).show()

References

[1]

O. C. Zienkiewicz, R. L. Taylor and J. Z. Zhu, The Finite Element Method: Its Basis and Fundamentals, 7th ed., Elsevier, 2013.

class felupe.BazantOh(n: int = 21)

Bases: Scheme

Quadrature scheme for a numeric integration of the surface of a unit sphere [1]_.

Parameters:

n (int, optional) – The number of quadrature points (default is 21).

Notes

The approximation is given by

\[\int_{\partial V} f(x) dA \approx \sum f(x_q) w_q\]

with quadrature points \(x_q\) and corresponding weights \(w_q\).

Examples

>>> import felupe as fem
>>> import pyvista as pv
>>>
>>> quadrature = fem.BazantOh(n=21)
>>>
>>> plotter = quadrature.plot(weighted=True)
>>> sphere = pv.Sphere(radius=1).clip(normal="z", invert=False)
>>> actor = plotter.add_mesh(sphere, opacity=0.3, color="white")
>>> plotter.show()

References

[1]

Bazant, Z. P., & Oh, B. H. (1986). Efficient Numerical Integration on the Surface of a Sphere. ZAMM ‐ Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, 66(1), 37-49. https://doi.org/10.1002/zamm.19860660108