Note
Go to the end to download the full example code.
Inflation of a hyperelastic balloon#
This example requires external packages.
pip install contique
With the help of contique it is possible to apply a numerical parameter continuation algorithm on any system of equilibrium equations. This advanced tutorial demonstrates the usage of FElupe in conjunction with contique. The unstable inflation of a rectangular hyperelastic balloon demonstrates this powerful approach. The deformed model and the pressure - displacement curve is plotted.
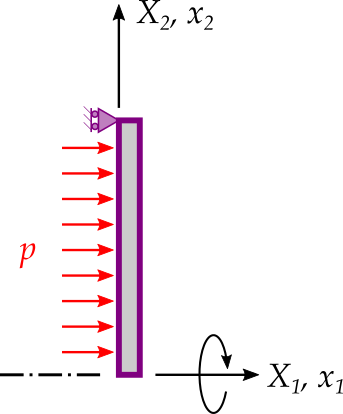
First, setup a problem in FElupe as usual (mesh, region, field, boundaries, umat, solid and a pressure boundary). For the material definition we use the Neo-Hooke built-in hyperelastic material formulation, see Eq. (1).
import contique
import numpy as np
import felupe as fem
mesh = fem.Cube(b=(25, 25, 1), n=(4, 4, 2))
region = fem.RegionHexahedron(mesh)
field = fem.FieldContainer([fem.Field(region, dim=3)])
bounds = fem.dof.symmetry(field[0], axes=(True, True, False))
bounds["fix-z"] = fem.Boundary(field[0], fx=25, fy=25, mode="or", skip=(1, 1, 0))
dof0, dof1 = fem.dof.partition(field, bounds)
umat = fem.Hyperelastic(fem.neo_hooke, mu=1)
solid = fem.SolidBodyNearlyIncompressible(umat, field, bulk=5000)
region_for_pressure = fem.RegionHexahedronBoundary(mesh, mask=(mesh.points[:, 2] == 0))
field_for_pressure = fem.FieldContainer([fem.Field(region_for_pressure, dim=3)])
pressure = fem.SolidBodyPressure(field_for_pressure)
The next step involves the problem definition for contique. For details have a look at its README.
def fun(x, lpf, *args):
"The system vector of equilibrium equations."
field[0].values.ravel()[dof1] = x
pressure.update(lpf)
return fem.tools.fun([solid, pressure], field)[dof1]
def dfundx(x, lpf, *args):
"""The jacobian of the system vector of equilibrium equations w.r.t. the
primary unknowns."""
K = fem.tools.jac([solid, pressure], field)
return fem.solve.partition(field, K, dof1, dof0)[2]
def dfundl(x, lpf, *args):
"""The jacobian of the system vector of equilibrium equations w.r.t. the
load proportionality factor."""
pressure.update(1)
return fem.tools.fun([pressure], field)[dof1]
Next we have to init the problem and specify the initial values of unknowns (the undeformed configuration). After each completed step of the numeric continuation the results are saved.
|Step,C.| Control Component | Norm (Iter.#) | Message |
|-------|-------------------|---------------|-------------|
| 1,1 | 66+ => 33+ | 6.0e+03 ( 8#) |Failed |
| 2,1 | 66+ => 0+ | 1.7e+02 ( 8#) |Failed |
| 3,1 | 66+ => 0+ | 6.8e-04 ( 8#) |Failed |
| 4,1 | 66+ => 0+ | 1.1e-08 ( 7#) | => re-Cycle |
| 2 | 0+ => 0+ | 1.4e-08 ( 3#) | |
| 5,1 | 0+ => 0+ | 7.6e-08 ( 4#) | |
| 6,1 | 0+ => 0+ | 6.7e-08 ( 4#) | |
| 7,1 | 0+ => 0+ | 5.0e-07 ( 4#) | |
| 8,1 | 0+ => 0+ | 3.3e-09 ( 5#) | |
| 9,1 | 0+ => 0+ | 8.2e-09 ( 5#) | |
| 10,1 | 0+ => 0+ | 4.5e-08 ( 5#) | |
| 11,1 | 0+ => 0+ | 4.0e-09 ( 6#) | |
| 12,1 | 0+ => 0+ | 2.6e-09 ( 8#) | |
| 13,1 | 0+ => 0+ | 1.6e-08 ( 7#) | |
| 14,1 | 0+ => 0+ | 3.7e-07 ( 7#) | |
| 15,1 | 0+ => 0+ | 2.8e-03 ( 8#) |Failed |
| 16,1 | 0+ => 0+ | 1.1e-10 ( 5#) | |
| 17,1 | 0+ => 0+ | 2.1e-10 ( 5#) | |
| 18,1 | 0+ => 0+ | 1.3e-10 ( 5#) | |
| 19,1 | 0+ => 0+ | 1.6e-08 ( 5#) | |
| 20,1 | 0+ => 0+ | 1.7e-10 ( 6#) | |
| 21,1 | 0+ => 0+ | 7.9e-08 ( 8#) | |
| 22,1 | 0+ => 0+ | 3.0e-06 ( 8#) |Failed |
| 23,1 | 0+ => 0+ | 9.3e-08 ( 4#) | |
| 24,1 | 0+ => 0+ | 1.5e-07 ( 4#) | |
| 25,1 | 0+ => 0+ | 2.2e-07 ( 4#) | |
| 26,1 | 0+ => 0+ | 1.7e-09 ( 5#) | |
| 27,1 | 0+ => 0+ | 2.5e-07 ( 5#) | |
| 28,1 | 0+ => 0+ | 1.5e-10 ( 6#) | |
| 29,1 | 0+ => 0+ | 7.7e-06 ( 8#) |Failed |
| 30,1 | 0+ => 0+ | 7.4e-07 ( 4#) | |
| 31,1 | 0+ => 0+ | 8.9e-07 ( 4#) | |
| 32,1 | 0+ => 0+ | 1.8e-10 ( 5#) | |
| 33,1 | 0+ => 0+ | 2.4e-09 ( 5#) | |
| 34,1 | 0+ => 0+ | 1.7e-07 ( 5#) | |
| 35,1 | 0+ => 0+ | 1.4e-10 ( 6#) | |
| 36,1 | 0+ => 0+ | 2.4e-07 ( 7#) | |
| 37,1 | 0+ => 0+ | 2.3e-03 ( 8#) |Failed |
| 38,1 | 0+ => 0+ | 2.2e-10 ( 5#) | |
| 39,1 | 0+ => 0+ | 3.5e-10 ( 5#) | |
| 40,1 | 0+ => 0+ | 2.8e-10 ( 5#) | |
| 41,1 | 0+ => 0+ | 7.4e-09 ( 5#) | |
| 42,1 | 0+ => 66+ | 2.9e-07 ( 5#) | => re-Cycle |
| 2 | 66+ => 66+ | 1.3e-10 ( 5#) | |
| 43,1 | 66+ => 66+ | 3.0e-10 ( 6#) | |
| 44,1 | 66+ => 66+ | 4.0e-10 ( 6#) | |
| 45,1 | 66+ => 66+ | 8.3e-09 ( 6#) | |
| 46,1 | 66+ => 66+ | 8.5e-08 ( 6#) | |
| 47,1 | 66+ => 66+ | 6.8e-07 ( 6#) | |
| 48,1 | 66+ => 66+ | 3.0e-10 ( 7#) | |
| 49,1 | 66+ => 66+ | 3.7e-10 ( 7#) | |
| 50,1 | 66+ => 66+ | 5.4e-10 ( 7#) | |
| 51,1 | 66+ => 66+ | 5.4e-07 ( 6#) | |
| 52,1 | 66+ => 66+ | 2.2e-10 ( 7#) | |
| 53,1 | 66+ => 66+ | 1.2e-10 ( 7#) | |
| 54,1 | 66+ => 66+ | 3.3e-10 ( 7#) | |
| 55,1 | 66+ => 66+ | 3.3e-10 ( 7#) | |
| 56,1 | 66+ => 66+ | 9.2e-07 ( 6#) | |
| 57,1 | 66+ => 66+ | 4.4e-10 ( 7#) | |
| 58,1 | 66+ => 66+ | 4.0e-10 ( 7#) | |
| 59,1 | 66+ => 66+ | 4.0e-10 ( 7#) | |
| 60,1 | 66+ => 66+ | 4.2e-10 ( 7#) | |
| 61,1 | 66+ => 66+ | 6.3e-10 ( 7#) | |
| 62,1 | 66+ => 66+ | 4.0e-10 ( 7#) | |
| 63,1 | 66+ => 66+ | 6.1e-10 ( 7#) | |
| 64,1 | 66+ => 66+ | 1.2e-09 ( 7#) | |
| 65,1 | 66+ => 66+ | 3.4e-09 ( 7#) | |
| 66,1 | 66+ => 66+ | 1.2e-08 ( 7#) | |
| 67,1 | 66+ => 66+ | 6.6e-08 ( 7#) | |
| 68,1 | 66+ => 66+ | 5.4e-07 ( 7#) | |
| 69,1 | 66+ => 66+ | 3.1e-10 ( 8#) | |
| 70,1 | 66+ => 66+ | 8.2e-08 ( 6#) | |
| 71,1 | 66+ => 66+ | 6.4e+00 ( 8#) |Failed |
| 72,1 | 66+ => 66+ | 1.1e-09 ( 5#) | |
| 73,1 | 66+ => 66+ | 1.7e-10 ( 5#) | |
| 74,1 | 66+ => 66+ | 1.0e-06 ( 4#) | |
| 75,1 | 66+ => 66+ | 2.9e-09 ( 5#) | |
| 76,1 | 66+ => 66+ | 5.9e-10 ( 6#) | |
| 77,1 | 66+ => 66+ | 4.0e-09 ( 8#) | |
| 78,1 | 66+ => 66+ | 1.9e-07 ( 6#) | |
| 79,1 | 66+ => 66+ | 8.4e+02 ( 8#) |Failed |
| 80,1 | 66+ => 66+ | 5.9e-10 ( 6#) | |
| 81,1 | 66+ => 66+ | 1.6e-09 ( 5#) | |
| 82,1 | 66+ => 66+ | 5.3e-09 ( 5#) | |
| 83,1 | 66+ => 66+ | 3.3e-10 ( 6#) | |
| 84,1 | 66+ => 66+ | 1.4e-07 ( 7#) | |
| 85,1 | 66+ => 66+ | 2.6e-10 ( 6#) | |
| 86,1 | 66+ => 66+ | 9.2e-08 ( 6#) | |
| 87,1 | 66+ => 66+ | 6.4e-09 ( 6#) | |
| 88,1 | 66+ => 66+ | 2.7e-08 ( 6#) | |
| 89,1 | 66+ => 66+ | 2.0e-09 ( 7#) | |
| 90,1 | 66+ => 66+ | 6.3e-09 ( 7#) | |
| 91,1 | 66+ => 26+ | 9.0e+04 ( 8#) |Failed |
| 92,1 | 66+ => 66+ | 3.0e-07 ( 5#) | |
| 93,1 | 66+ => 66+ | 8.5e-10 ( 7#) | |
| 94,1 | 66+ => 66+ | 1.2e-09 ( 7#) | |
| 95,1 | 66+ => 66+ | 5.8e-07 ( 7#) | |
| 96,1 | 66+ => 31- | 1.4e+06 ( 8#) |Failed |
| 97,1 | 66+ => 66+ | 2.0e-09 ( 8#) | |
| 98,1 | 66+ => 43+ | 2.7e+09 ( 8#) |Failed |
| 99,1 | 66+ => 0+ | 1.7e-05 ( 8#) |Failed |
| 100,1 | 66+ => 0+ | 5.5e-09 ( 7#) | => re-Cycle |
| 2 | 0+ => 0+ | 1.1e-09 ( 5#) | |
| 101,1 | 0+ => 66- | 5.1e+06 ( 8#) |Failed |
| 102,1 | 0+ => 66+ | 1.1e+14 ( 8#) |Failed |
| 103,1 | 0+ => 66+ | 9.4e+04 ( 8#) |Failed |
| 104,1 | 0+ => 0+ | 2.4e-09 ( 6#) | |
| 105,1 | 0+ => 0+ | 1.8e-08 ( 3#) | |
| 106,1 | 0+ => 0+ | 1.6e-08 ( 3#) | |
| 107,1 | 0+ => 0+ | 1.0e-07 ( 3#) | |
| 108,1 | 0+ => 0+ | 5.7e-07 ( 3#) | |
| 109,1 | 0+ => 0+ | 2.3e-09 ( 4#) | |
| 110,1 | 0+ => 0+ | 1.4e-09 ( 4#) | |
| 111,1 | 0+ => 0+ | 3.5e-08 ( 4#) | |
| 112,1 | 0+ => 0+ | 8.4e-07 ( 4#) | |
| 113,1 | 0+ => 0+ | 3.7e-09 ( 5#) | |
| 114,1 | 0+ => 0+ | 1.1e-07 ( 5#) | |
| 115,1 | 0+ => 0+ | 2.3e-08 ( 6#) | |
| 116,1 | 0+ => 0+ | 6.2e-07 ( 6#) | |
| 117,1 | 0+ => 0+ | 4.7e-08 ( 8#) | |
| 118,1 | 0+ => 0+ | 2.6e-08 ( 8#) | |
| 119,1 | 0+ => 66+ | 2.5e+13 ( 8#) |Failed |
| 120,1 | 0+ => 66+ | 1.8e+03 ( 8#) |Failed |
| 121,1 | 0+ => 0+ | 6.0e-08 ( 4#) | |
| 122,1 | 0+ => 0+ | 5.1e-09 ( 4#) | |
| 123,1 | 0+ => 0+ | 4.4e-09 ( 4#) | |
| 124,1 | 0+ => 0+ | 8.6e-09 ( 4#) | |
| 125,1 | 0+ => 0+ | 1.1e-07 ( 4#) | |
| 126,1 | 0+ => 0+ | 3.1e-09 ( 5#) | |
| 127,1 | 0+ => 0+ | 5.6e-09 ( 5#) | |
| 128,1 | 0+ => 0+ | 6.3e-08 ( 5#) | |
| 129,1 | 0+ => 0+ | 1.5e-09 ( 6#) | |
| 130,1 | 0+ => 0+ | 2.3e-07 ( 6#) | |
| 131,1 | 0+ => 66+ | 6.3e+04 ( 8#) |Failed |
| 132,1 | 0+ => 0+ | 7.9e-09 ( 5#) | |
| 133,1 | 0+ => 0+ | 2.7e-09 ( 5#) | |
| 134,1 | 0+ => 0+ | 2.2e-09 ( 5#) | |
| 135,1 | 0+ => 0+ | 4.0e-09 ( 5#) | |
| 136,1 | 0+ => 0+ | 7.0e-08 ( 5#) | |
| 137,1 | 0+ => 66- | 4.1e+03 ( 8#) |Failed |
| 138,1 | 0+ => 0+ | 3.6e-09 ( 6#) | |
| 139,1 | 0+ => 0+ | 4.7e-07 ( 4#) | |
| 140,1 | 0+ => 0+ | 4.6e-07 ( 4#) | |
| 141,1 | 0+ => 0+ | 6.6e-09 ( 5#) | |
| 142,1 | 0+ => 0+ | 5.0e-09 ( 5#) | |
| 143,1 | 0+ => 0+ | 2.0e-08 ( 5#) | |
| 144,1 | 0+ => 0+ | 5.3e-07 ( 7#) | |
| 145,1 | 0+ => 0+ | 4.5e-07 ( 6#) | |
| 146,1 | 0+ => 66- | 2.7e+05 ( 8#) |Failed |
| 147,1 | 0+ => 0+ | 1.5e-09 ( 6#) | |
| 148,1 | 0+ => 0+ | 3.0e-09 ( 5#) | |
| 149,1 | 0+ => 0+ | 1.2e-08 ( 5#) | |
| 150,1 | 0+ => 0+ | 4.3e-09 ( 5#) | |
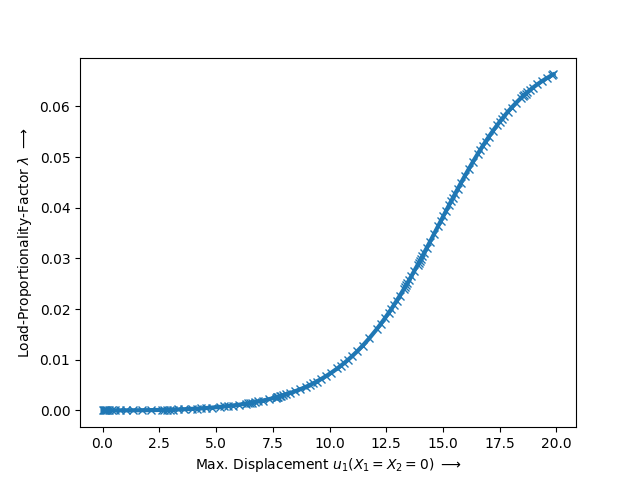
The unstable pressure-controlled equilibrium path is plotted as pressure-displacement curve.
import matplotlib.pyplot as plt
plt.plot(X[:, 2], X[:, -1], lw=3)
plt.xlabel(r"Max. Displacement $u_3(X_1=X_2=X_3=0)$ $\longrightarrow$")
plt.ylabel(r"Load-Proportionality-Factor $\lambda$ $\longrightarrow$")
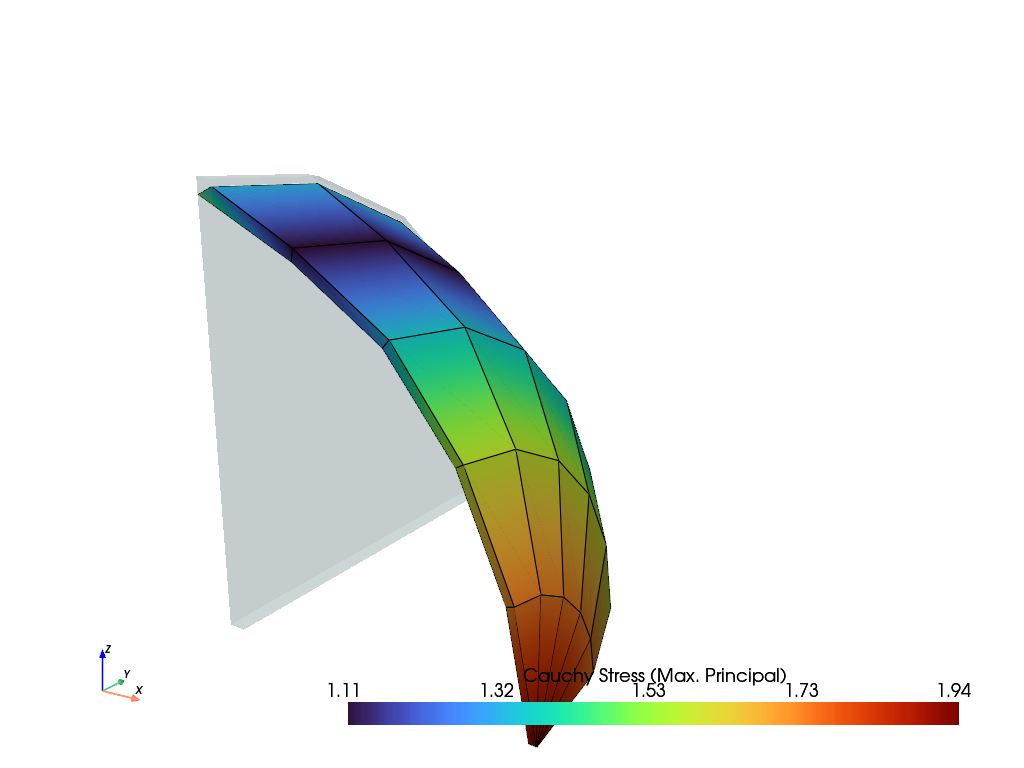
The deformed configuration of the solid body is plotted.
solid.plot("Principal Values of Cauchy Stress").show()
Total running time of the script: (0 minutes 16.707 seconds)